مقدمة
في هذا المقال سنتحدث عن خوارزمية النزول التدريجي او (Gradient Descent) وهي تعد اشهر الطرق و اكثرها استخداما في حل المعادلات المستخدمة في خوارزميات تعلم الآلة (machine learning) و كذلك التعلم العميق (deep learning).
سوف نتعرض لكيفية عمل النزول التدريجي و اهميته و المشاكل التي نتعرض لها مع استخدامه و كيف ان هناك بعض التحديثات عليه التي تمكننا من ان نتفادى هذه المشاكل و ان نحصل على نتائج افضل.
المصدر
ما هو النزول التدريجي
كما تحدثنا من قبل في مقالنا السابق عن كيفية تعلم الآلة والذي يمكنك الإطلاع عليه من
هنا، ان وظيفة النزول التدريجي هو تقليل معدل الخطأ في توقعاتنا و التي هي ناتجة بالاساس من استخدام بعض الأوزان.
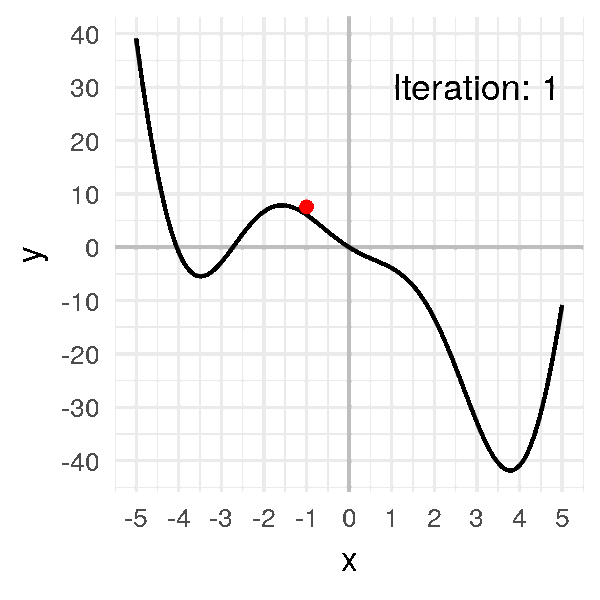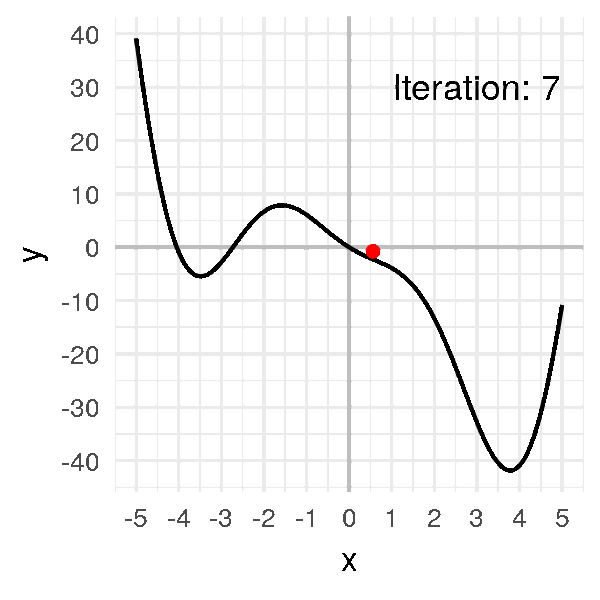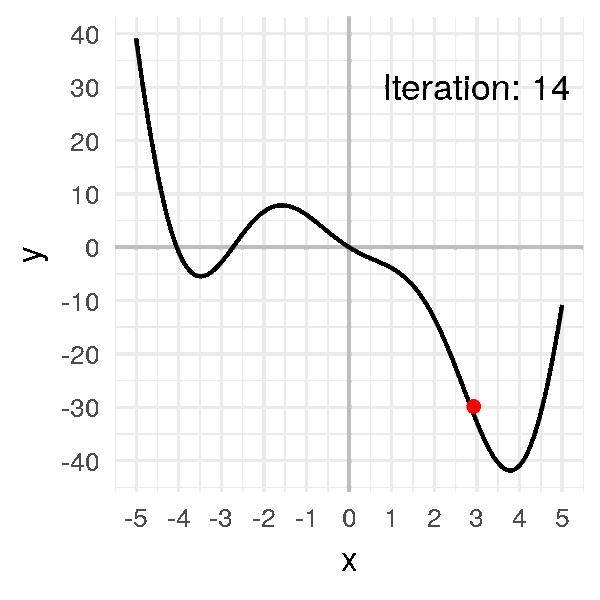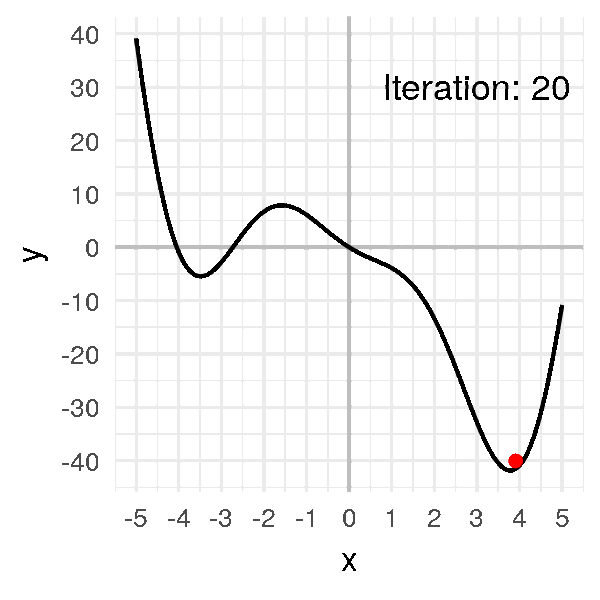
يمكنك تخيل المشكلة كأنك على سطح جبل ما ولا ترى حولك بسبب الضباب و لكنك تريد النزول، حينئذا ستتحسس طريقك و تبحث عن اتجاه الانخفاض وتبدأ في التحرك من خلاله، هذا ما يفعله بالضبط النزول التدريجي، اذ انه يبحث ايضا في كل اتجاه (بالنسبة لنا هنا كل اتجاه يمثل وزن من الاوزان) اين يجب ان تكون خطوته القادمة؟ يمين؟ يسار؟ امام ؟ ام خلف ؟.

المصدر
نظرة داخل النزول التدريجي
دعنا ننظر عن كثب كيف يعمل هذا النزول التدريجي
$$w_t = w_{t-1} - \eta \frac{\partial }{\partial w}E(w)$$
كما تتذكر من المقال السابق هذه كانت معادلة النزول التدريجي و هي بإختصار اننا سوف نرى ما معدل الخطأ الذي قمنا به ثم نرى كيف يمكننا ان نحسن هذا الخطأ عن طريق حساب معدل التغير (التفاضل) ثم نقوم بتغيير الوزن القديم بما هو قيمته سالب التفاضل (لان التفاضل يشير لإتجاه الزيادة) بمعامل η والذي يعبر عن معدل التعلم او (learning rate) دعنا نرى هذه المعادلة بالرسم لنستوضح اكثر
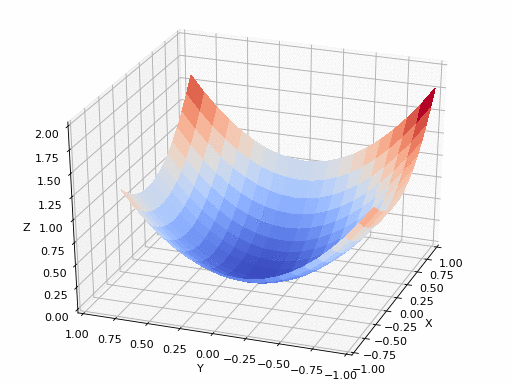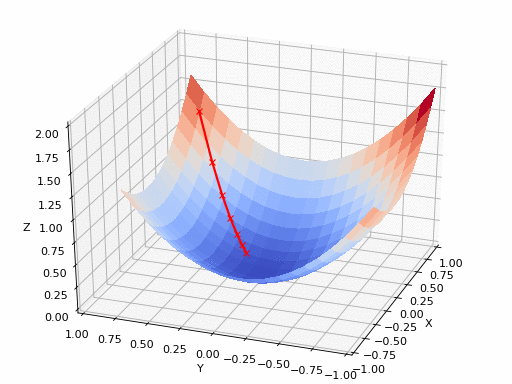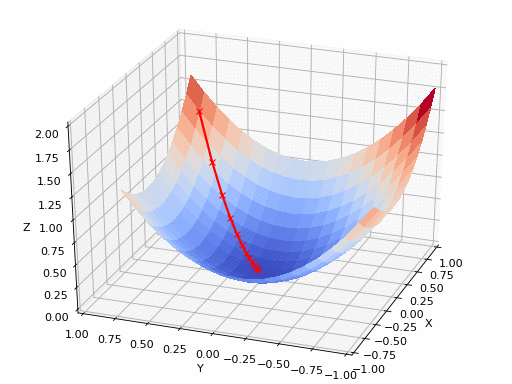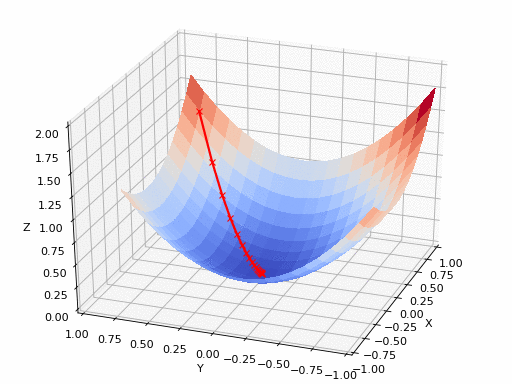
المصدر
الرسم بالأعلى يظهر كيف يقوم النزول التدريجي بإيجاد اقل نقطة في الدالة و التي لونها ازرق هنا، ولكن يمكن ايضا ان ترى اشكال توضيحية للنزول التدريجي في شكل ما يسمى (contours) وهي تعبر عن الشكل الذي رأيناه باﻷعلى ولكن اذا قمنا بقطع شريحة افقية به او نظرنا إليه من أعلى و سيصبح شكله كما يلي.

المصدر
هنا يتضح لنا كيف ان الرسم الثنائي الابعاد (contour) ماهو الا شريحة من الرسم الثلاثي الأبعاد لذا ان رأيت رسم بهذا الشكل فلا تقلق انها تعبر عن نفس الشئ.
النزول التدريجي العشوائي (Stochastic Gradient Descent)
النزول التدريجي يحتاج إلى حساب معدل التغيير كما رأينا من قبل، وفي الاعدادات العادية يتم حساب الخطأ بناءا على كل ما توقعناه كما رأينا مسبقا وهذا يعطينا نظرة شاملة عن الخطأ في جميع البيانات التي لدينا ولكن عندما يصبح حجم هذه البيانات كبير جدا يصبح الوضع بطئ للغاية لانه عند كل عملية تحديث للوزن سوف نضطر إلى حساب الخطأ في جميع البيانات المتاحة و بالتالي تصبح عملية التعلم بشكل عام ابطئ بكثير، لذلك يوجد اقتراح افضل و هو ان تقوم بأخذ الخطأ من مثال واحد من البيانات و نرى اين يمكننا ان نتحرك، بالطبع سيخطر ببالك ان ربما يكون هذا التحرك في اتجاه خاطئ لان هذا المثال الذي قمنا بإختياره ليس ممثل للبيانات كلها و هذا صحيح ويتسبب في ان تكون عملية النزول عشوائية قليلا ولكن في المجمل هي عملية نزول مازالت، ولكن في المقابل تصبح عملية النزول اسرع بكثير.
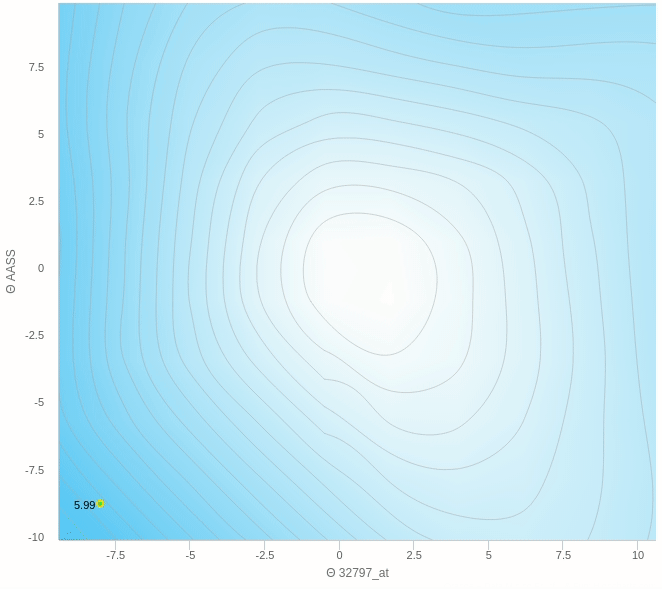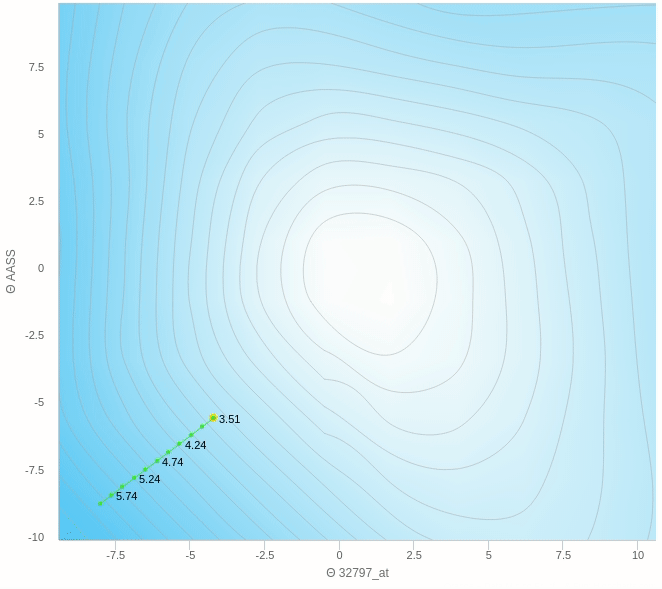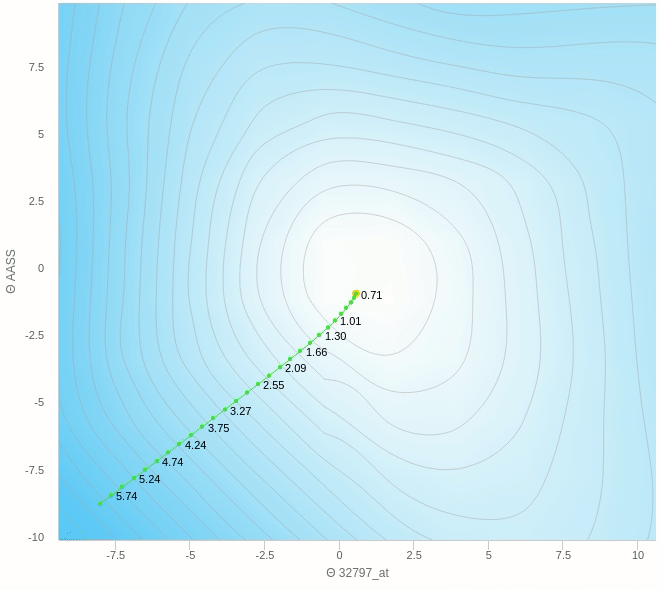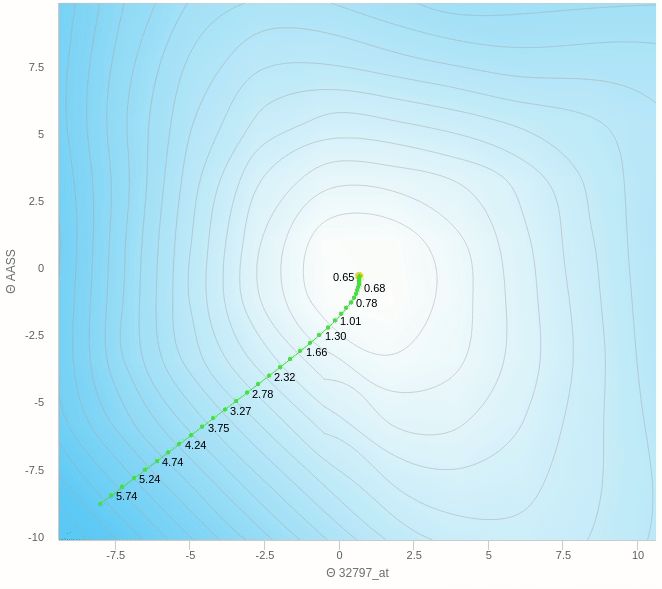
هنا نرى كيف يقوم النزول التدريجي بالنزول تدريجيا بخطوات ثابتة نحو الهدف و هو اقل قيمة في الدالة كما نراها تعالى نرى على الناحية الاخرى النزول التدريجي العشوائي.
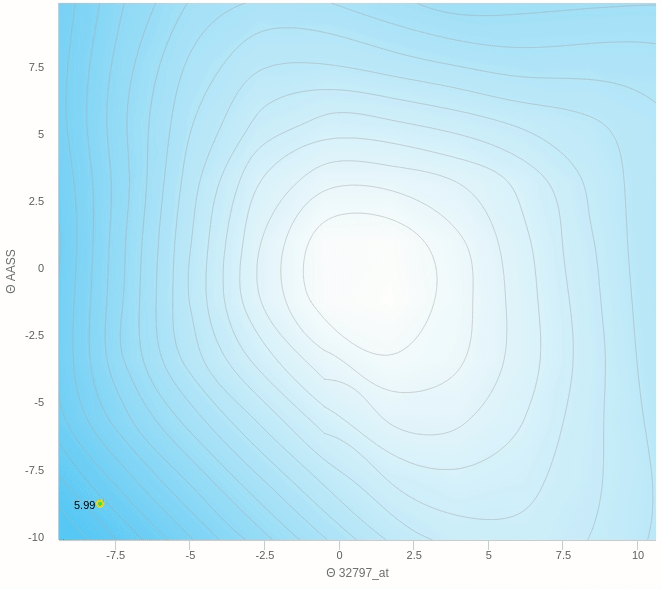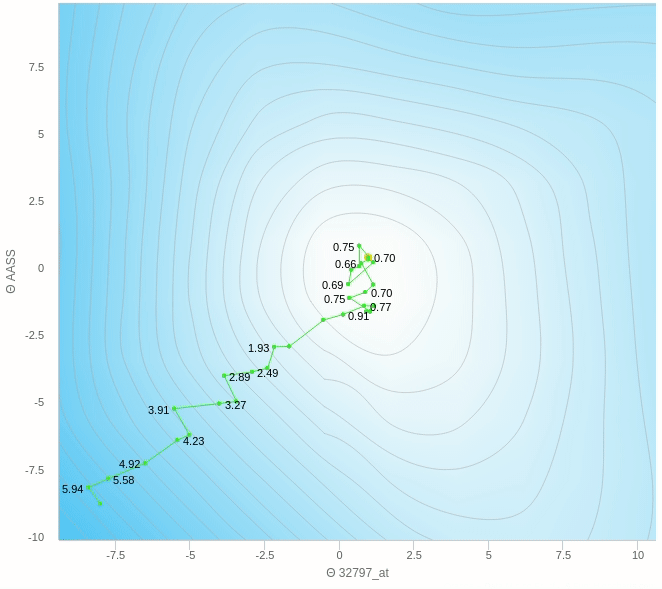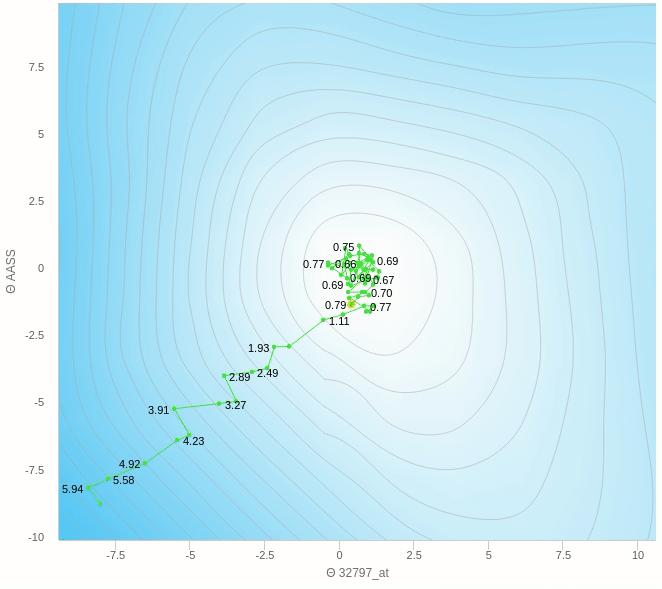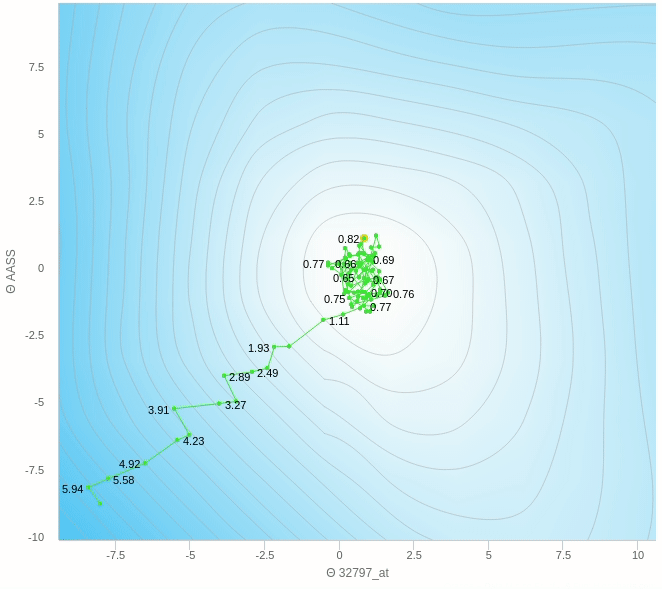
يمكنك ملاحظة عدة اشياء هنا، مثل ان الخطوات التي يتبعها النزول ليست بالضرورة كلها صحيحة فهو يحيد في بعض الخطوات و ايضا عندما يقترب من النقطة المطلوبة يبدأ في التقلب بعيدا عن الهدف ولا يصل إلى الهدف مرة واحدة وهذا من عيوب هذه الطريقة.
النزول التدريجي المجزء (Mini-Batch Gradient Descent)
هنا الفكرة الرئيسية هي ان تقوم بعمل خطوات تدريجية ايضا بنفس المبدأ السابق العشوائي ولكن بدل من ان نقوم بالتحرك على اساس خطوة واحدة سوف نختار عدد معين من العينات و نأخذ الخطأ بناءا عليهم ثم نقوم بتحديث الأخطاء و هكذا نتغلب على مشكلة العشوائية الناجمة عن اختاير نقطة واحدة ولكن بالطبع سيظل هناك جزء من الخطأ عن الطريقة التقليدية ولكن هذه الطريقة تساعد كما وضحنا في سرعة العملية و كذلك الاتجاه الذي يسير فيه الاوزان.
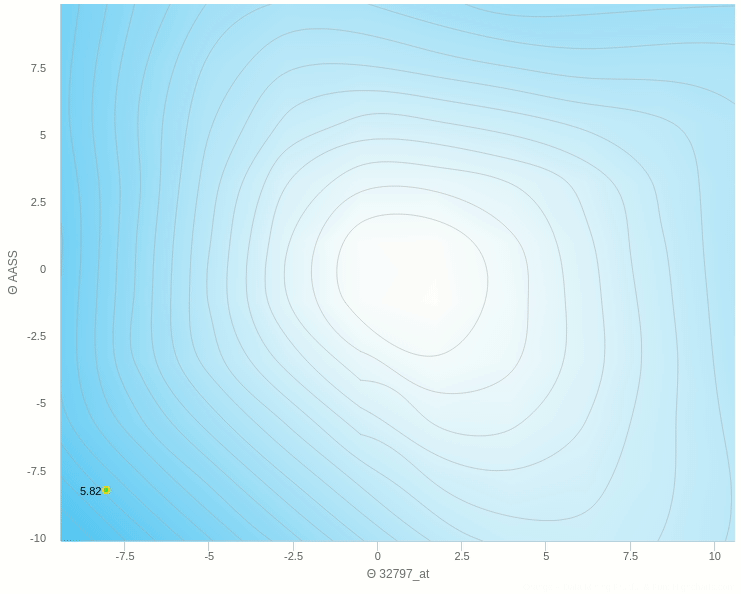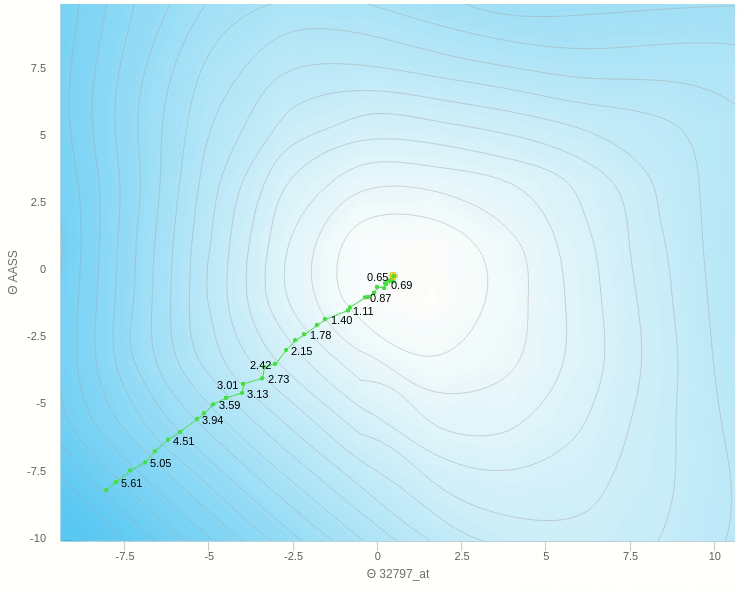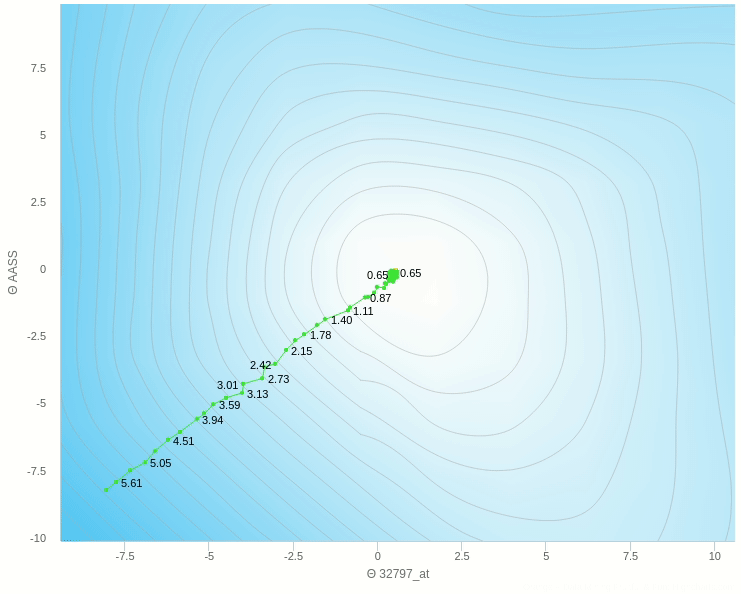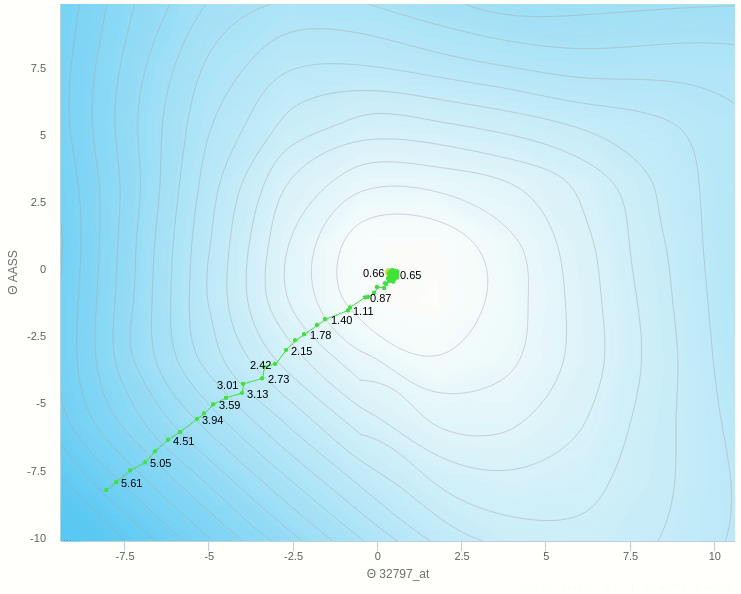
يمكنك ان ترى هنا بعض العشوائية في المنتصف ولكنها اقل بكثير من النموذج حيث تم التحديث بناءا على عينة واحدة فهنا نقوم بعمل الخطوة بناءا على 5 عينات فقط وطبعا كلما زاد هذا العدد كلما كانت خطواتنا ادق.
قيمة التفاضل قد تخدعك في بعض الأحيان

المصدر
احيانا يكون التوجه العام للنزول لدينا صحيح ولكن عند بعض النقاط نجد ان التفاضل يدفعنا لأماكن مختلفة عن كل التفاضلات السابقة، ففي هذه الحالة نريد ان نقوم بتقييم النزول وعندما نجد ان هناك خطوة غير منطقية لا نتبعها بشكل مباشر و انما ندع الأمر للنقاط السابقة ايضا حتى تحدد هل هذا الاتجاه صحيح بشكل كلي ام يجب الا نذهب في هذا الأتجاه.
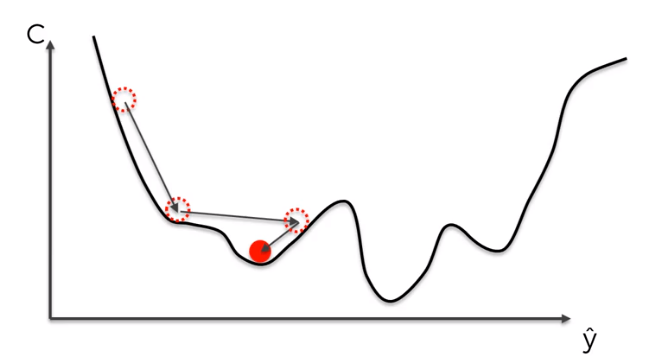
المصدر
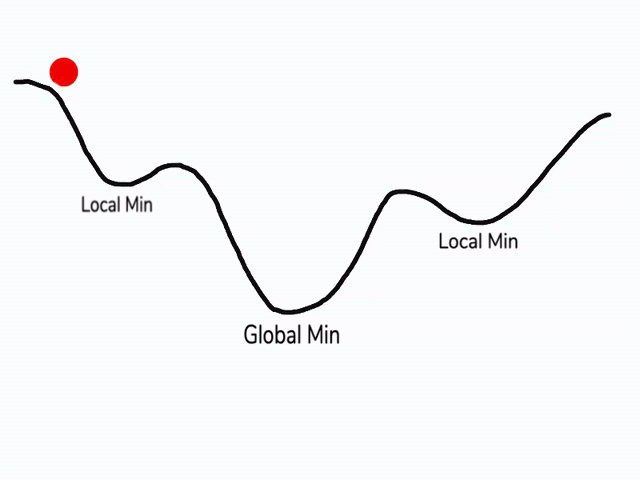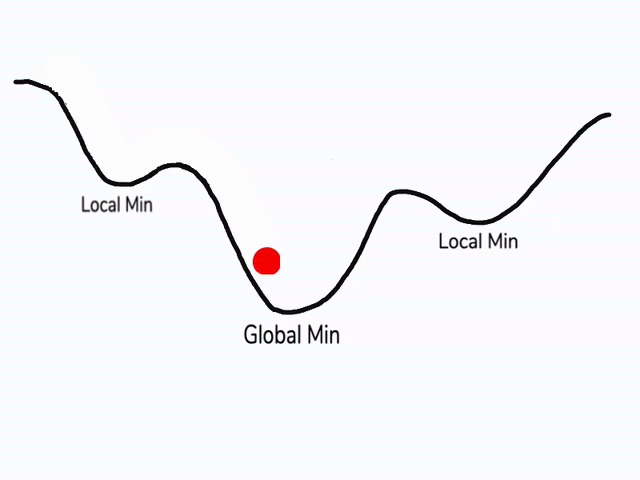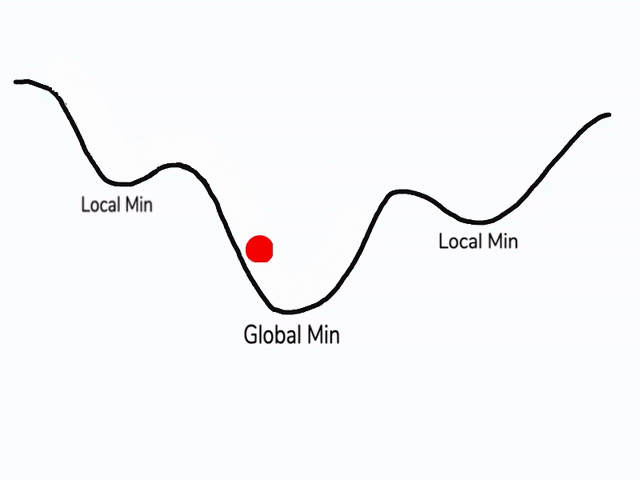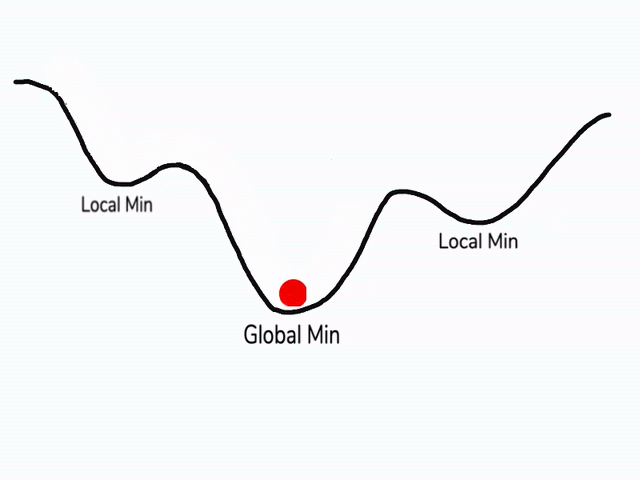
ايضا في بعض المناطق في دالتنا قد تجد اماكن تسمى الصغرى المحلية (local minimum) و ايضا الصغرى العظمى (global minimum) وقد نظن اثناء النزول ان النقاط الصغرى المحلية هي اصغر نقطة لان التفاضل سيبقينا في النقطة المحلية، ولكن نحن نحتاج إلى طريقة تمكننا من الهروب من هذه النقطة المحلية و النزول في الصغرى العظمى، فيما يلي سوف نستعرض طرق لحل هذه المشكلة.
استخدام قوة الدفع (Momentum)
المصدر
تقوم هذه الطريقة على مبدأ قوة الدفع كأنك تلقي بكرة من فوق تلة، اثناء انزلاقها سوف تحصل على قوة دفع تزداد مع الوقت وسوف تصبح مع الوقت سريعة بحيث لا يمكن ان تقف في حفرة صغيرة في طريقها و انما ستتوقف فقط عند نهاية هذه التلة، هذه بالضبط هي نظرية عمل قوة الدفع في النزول التدريجي ايضا ولكن هنا الكرة هي قيمة الأوزان و التلة هي الخطأ و سوف نستخدم الخطوات السابقة حتى تصبح داعما لنا و كذلك تزيد من الدفع للأوزان نحو النقطة الصغرى العظمى.
دعنا نسترجع معادلة النزول التدريجي التي ذكرناها و نرى كيف يمكننا تعديلها لتتضمن مبدأ الدفع هذا
$$ w_t = w_{t-1} - \eta \frac{\partial}{\partial w}Error(w)$$
سنقوم الآن بتعريف المعادلة الجديدة التي سوف نستخدمها
$$ w_t = w_{t-1} - h_t $$
إذا التحديث الذي يحدث على الاوزان الآن اصبح متغير، دعنا نرى اذا ماهو المتغير الجديد h
$$ h_t = \alpha h_{t-1} + \eta g_t $$
$$ g_t = \frac{\partial}{\partial w}Error(w) $$
هنا يمكنك ان ترى اننا اختصرنا التفاضل لرمز g لتسهيل العملية و الآن دعنا نتحدث عن هذه الرموز الجديدة.
هنا الرمز α هو متغير تقوم بتحديده مسبقا و هو في المعادلة هنا يعبر عن اهمية ht-1 في المعادلة و غالبا ما تكون قيمته 0.9 اذا التحديث الجديد للأوزان مازال كما هو فيما يخص الجزء الثاني من المعادلة و انما هناك جزء جديد تم اضافته و هو محصلة h فإن المعادلة ببساطة تقوم بجمع قيمة h على مدار مرات التعلم (iterations) و بالتالي عند كل خطوة سيكون اتجاهك متوقف على التفاضل و لكن ايضا متوقف على كل الخطوات السابقة فان معادلة h يمكنك ان تفكر فيها على هذا النحو مثلا عند الخطوة الثانية
$$ h_2 = 0.9( 0.9( 0.9*0 + \eta g_0 ) + \eta g_1 ) + \eta g_2$$
كما ترى هنا هي ببساطة تراكم كل ما سبق من خطوات مع اضافة المعامل α والذي يمكنك ان تفكر فيه على انه معامل الاحتكاك اثناء النزول لان كلما قل هذا المعامل صار الاعتماد على التفاضل الحالي فقط اي لا قوة دفع و كلما زاد المعامل واقترب من 1 صار الاحتكاك اقل ما يمكن وخطوتك ستزداد بمقدار h والذي يحمل كل الخطوات السابقة.
لاحظ هنا ايضا انه اذا في مرحلة ما كان التفاضل بقيمة مخالفة لكل ما سبق على سبيل المثال تفاضل قيمته سالبة على عكس ما سبقه كلهم، حينئذ يعادل طرفي المعادلة بعضهم لان العزم بالفعل له تأثير قوي على خطوتنا و ان كانت الخطوة مخالفة للعزم فغالبا سوف تقل قيمتها وقد تتم تجاهلها، يشبه الامر ان تكون الكرة منزلقة من قمة المنحدر و قام احد بدفعها للاعلى ربما ترتفع قليلا ولكن لن تغير اتجاهها بسب الدفع الحاصل عليها بالفعل و ايضا بنفس المبدأ اذا سقطت في حفرة صغرى محلية سوف تهرب منها بسهولة و تكمل نزولها نحو الصغرى العظمى.
تفاضل نستروف المتسارع (NAG)
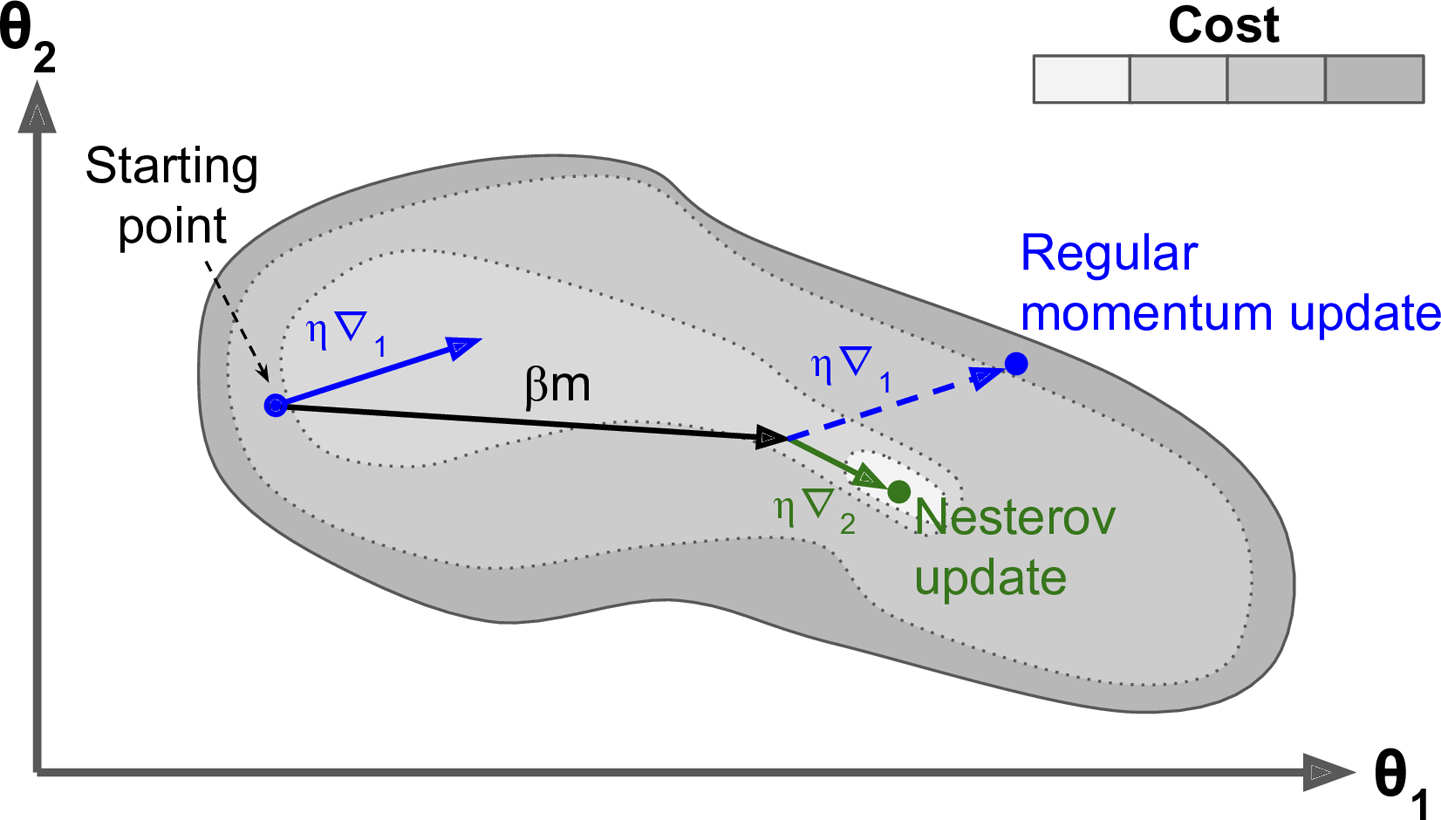
المصدر
قام يوري نستروف بعمل تعديل بسيط في طريقة التدافع تمكننا من تسريع العملية وكذلك الحصول على نتائج افضل، و الطريقة ببساطة هي ان نسمح للنقطة بالتحرك في اتجاه التدافع اولا ثم نقوم بحساب التفاضل من هناك ثم نتحرك يشبه الأمر نفس عملية النزول ولكن الفرق انك تترك التدافع ليصل بك إلى مكان ما ثم تبدأ في اختيار خطوتك التالية، يمكنك رؤية هذا في المعادلات التالية
$$ h_t = \alpha h_{t-1} + \eta \frac{\partial}{\partial w}( w_{t-1} - \alpha h_{t-1}) $$
$$ w_t = w_{t-1} - h_t $$
هنا كما سبق نقوم بتحديث الاوزان باستخدام المتغير h كما سبق ولكن الاختلاف في المعادلة الاولى، ولاحظ هنا كيف يتم اخد خطوة في اتجاه التدافع اولا
$$ w_{t-1} - \alpha h_{t-1} $$
و من ثم نرى من عند النقطة الناتجة ما هو افضل اتجاه يمكننا ان نسلكه
$$ \eta \frac{\partial}{\partial w}( w_{t-1} - \alpha h_{t-1}) $$
و نقوم بجمع هذه القيم على مدار خطواتنا مع الأخذ في الاعتبار طبعا معامل الاحتكاك α.
تعتبر هذه الطريقة اسرع وافضل من التدافع الاعتيادي و سميت باسم نستروف نسبة إلى مخترعها.
ماذا عن معدل التعلم η (learning rate)
في الطرق السابقة تلاحظ عدم تطرقنا لمعامل التعلم وهو في الحقيقة مهم جدا، تعالى نرى تأثيره مبدأيا في عملية التعلم.
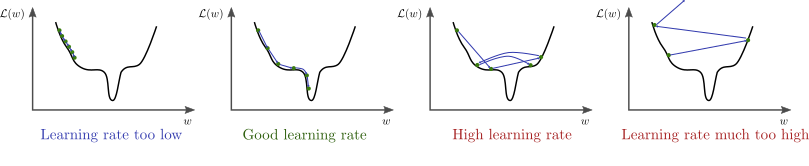
المصدر
تذكر ان التغيير الرئيسي للاوزان يحدث من خلال معامل التعلم، لان الاتجاه يأتي من التفاضل، ثم يقوم معدل التعلم بتحديد حجم الخطوة المراد التحرك بها
$$ w_t = w_{t-1} - \eta g_t $$
حيث g هو مقدار التفاضل لذلك فإن معدل التعلم قيمته مهمة جدا إذ ان قيمته اذا زادت فلن نصل إلى الحل الأمثل لان الخطوة المتخذة في الاتجاه الصحيح اكبر بكثير من اللازم و اذا كانت الخطوة صغيرة جدا فسنأخذ الكثير من الوقت حتى نصل إلى النقطة المناسبة إذا نحتاج لإيجاد حل مناسب هنا.
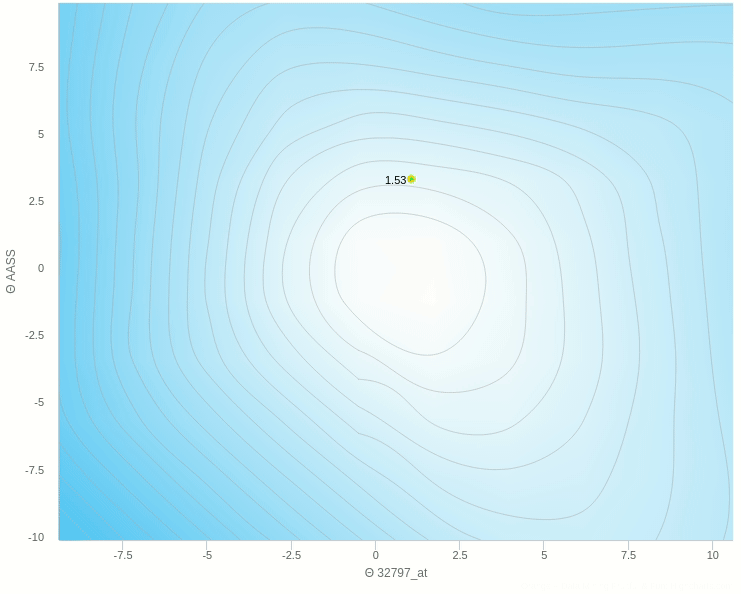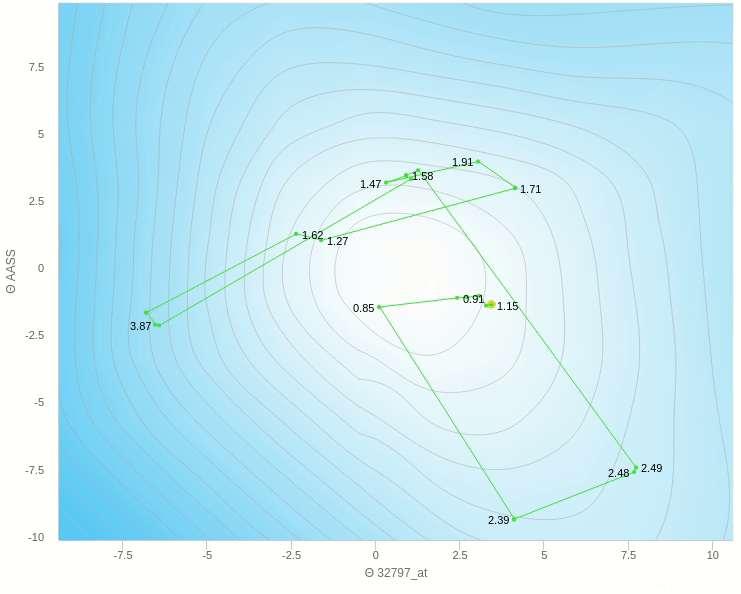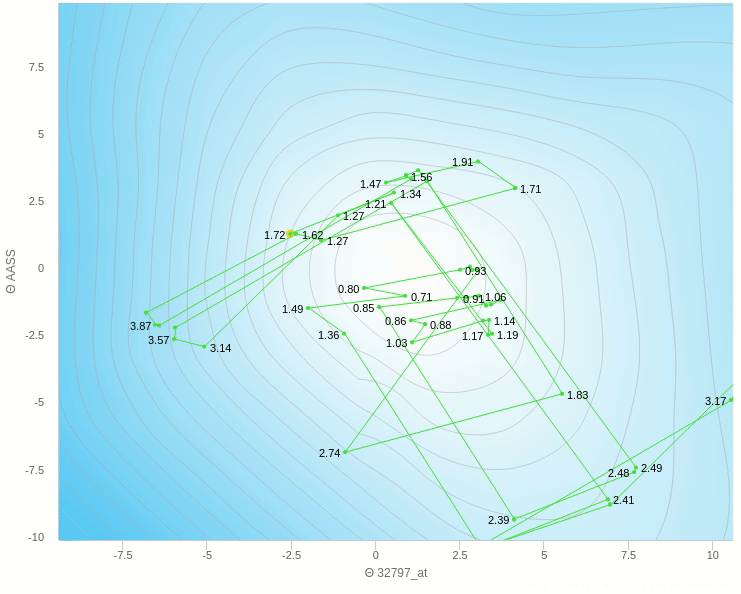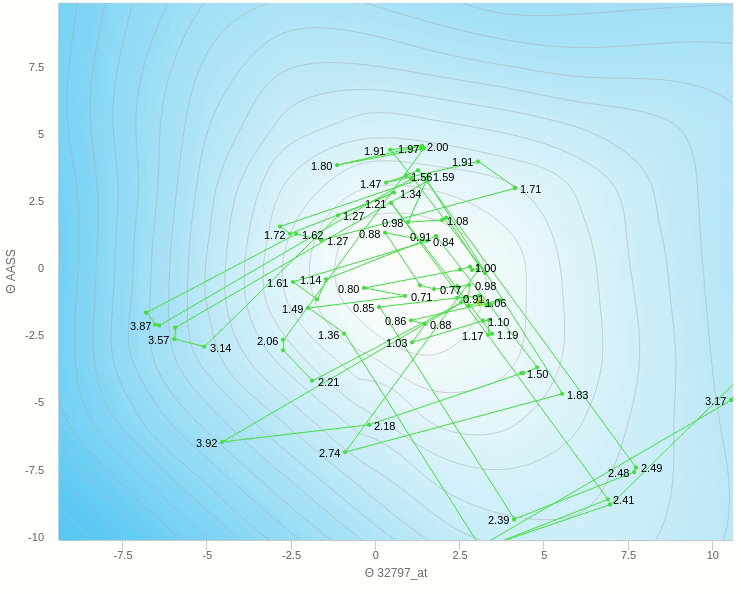
في الشكل السابق يظهر تأثير معدل التعلم عندما تكون قيمته كبيرة نسبيا فإن خطواته تكون صحيحة في اتجاهها ولكن لان حجم الخطوة كبير فإنه يقفز مسافة طويلة ولا يستقر في المكان الصحيح
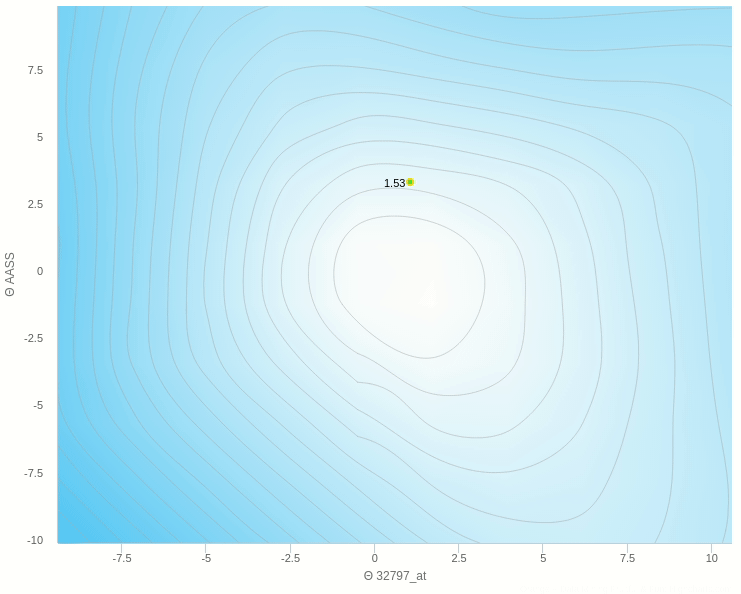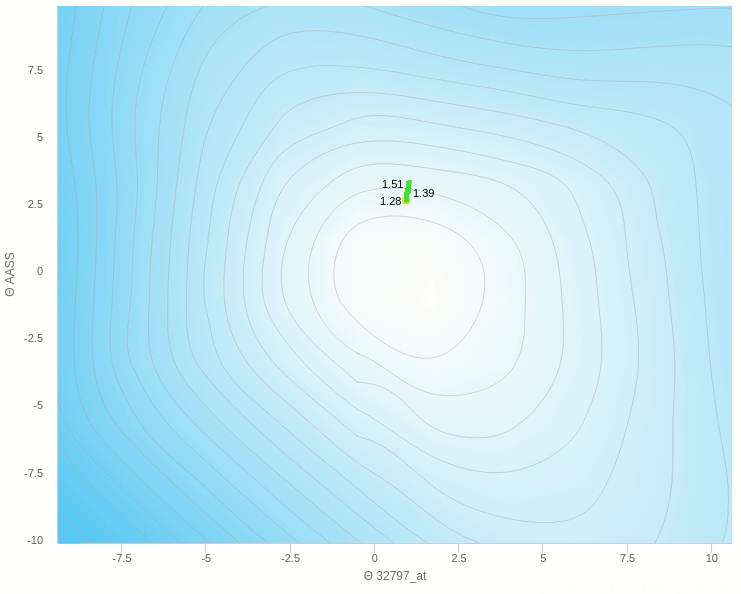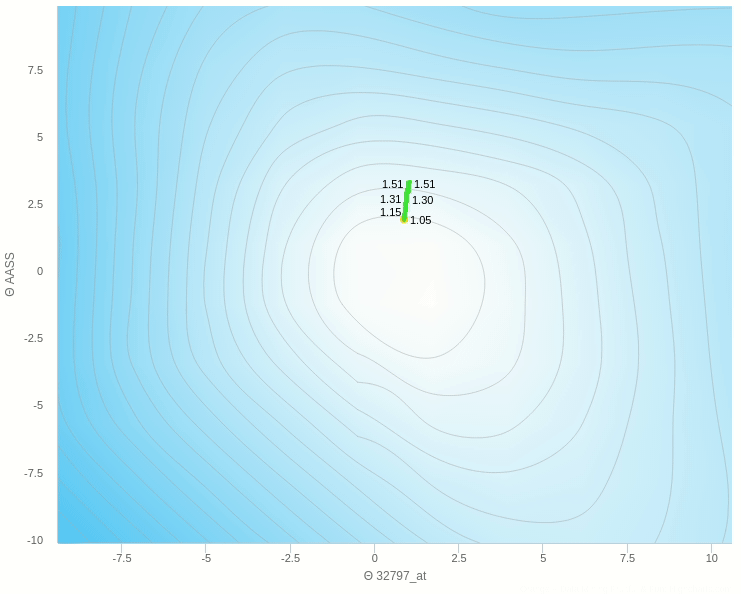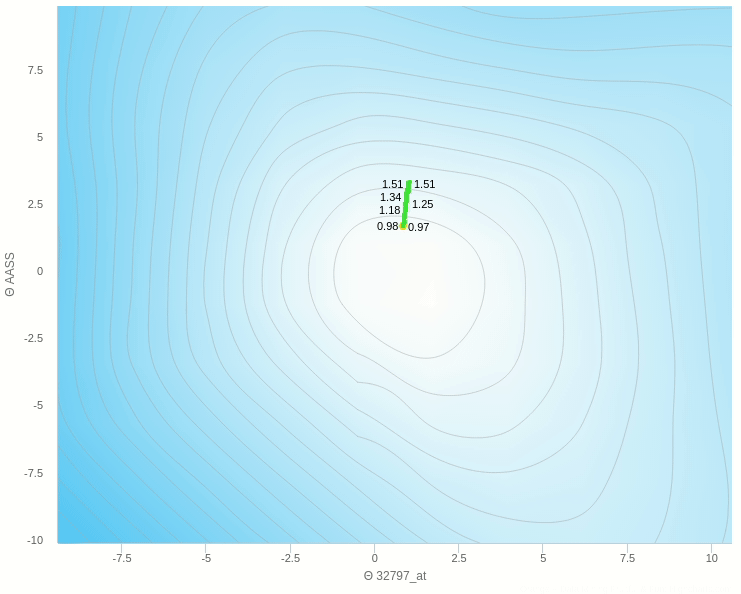
و هنا نرى انه عندما يكون معدل التغيير صغير للغاية تكون عملية التعلم بطيئة للغاية وبالتأكيد يكون توقف التحرك في المناطق الصغرى المحلية وارد جدا.
اذا ما الحل الأمثل؟ هل نختار قيمة صغيرة لمعدل التعلم ام نستخدم قيمة كبيرة له ؟
في حقيقة الأمر نحن نحتاج كلاهما، نحتاج خطوات كبيرة في بادئ الأمر ثم نتحرك بخطى اصغر كلما تقدمنا في التدريب او التعلم و هذا ما سنتعرض له في الفقرة التالية باستخدام التفاضل التكيفي (Adaptive Gradient AdaGrad)
التفاضل التكيفي (AdaGrad)
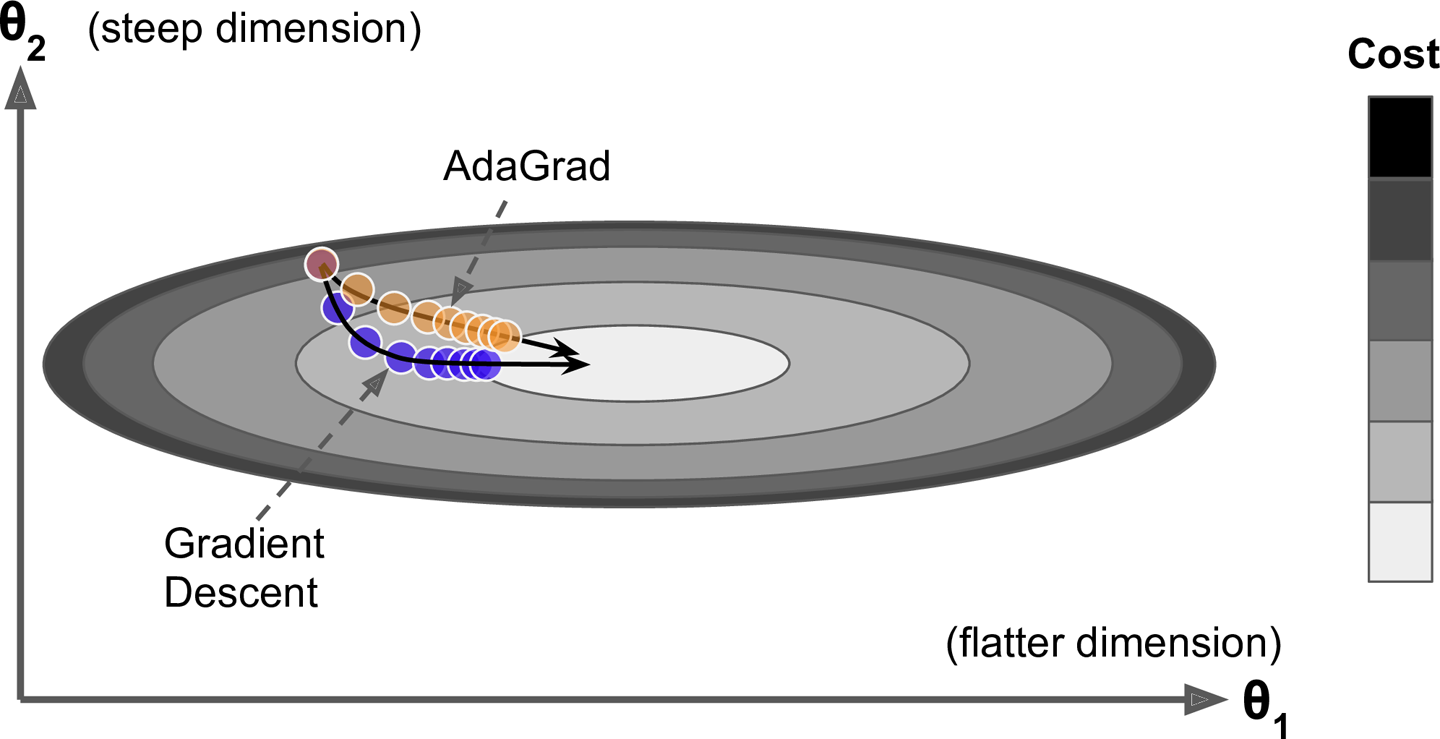
المصدر
هذه المرة سيكون تركيزنا بالأساس مع معامل التعلم (learning rate) وسنعتمد سياسة الإضمحلال بمعنى ان معدل التعلم سيبدأ بقيمة كبيرة ثم يبدأ في النقصان كلما تحركنا، ولكن ليس لكل الاتجاهات بالمثل، ولكن سنعتمد على خطوة مختلفة لكل اتجاه، بمعنى اننا سوف نقلل المعدل للإتجاهات التي بها انزلاق شديد حتى لاتؤثر على الإتجاه العام لانه كما ترى من الرسم اعلاه ان المحور الرأسي ان اتبعنا التفاضل القائم عليه (كما تعلم نحن نقوم بحساب التفاضل على كل اتجاه) واتبعنا خطواته ستجد انه سوف يأخذنا في منحنى بعيد قليلا عن الهدف ثم نبدا بعد ذلك في التحرك للهدف، ولكن باستخدام التفاضل التكيفي سوف نخفض معدل التغير لهذا المحور ونبقى على المحور الاخر بالتالي نتجه ناحية الهدف بشكل اسرع.
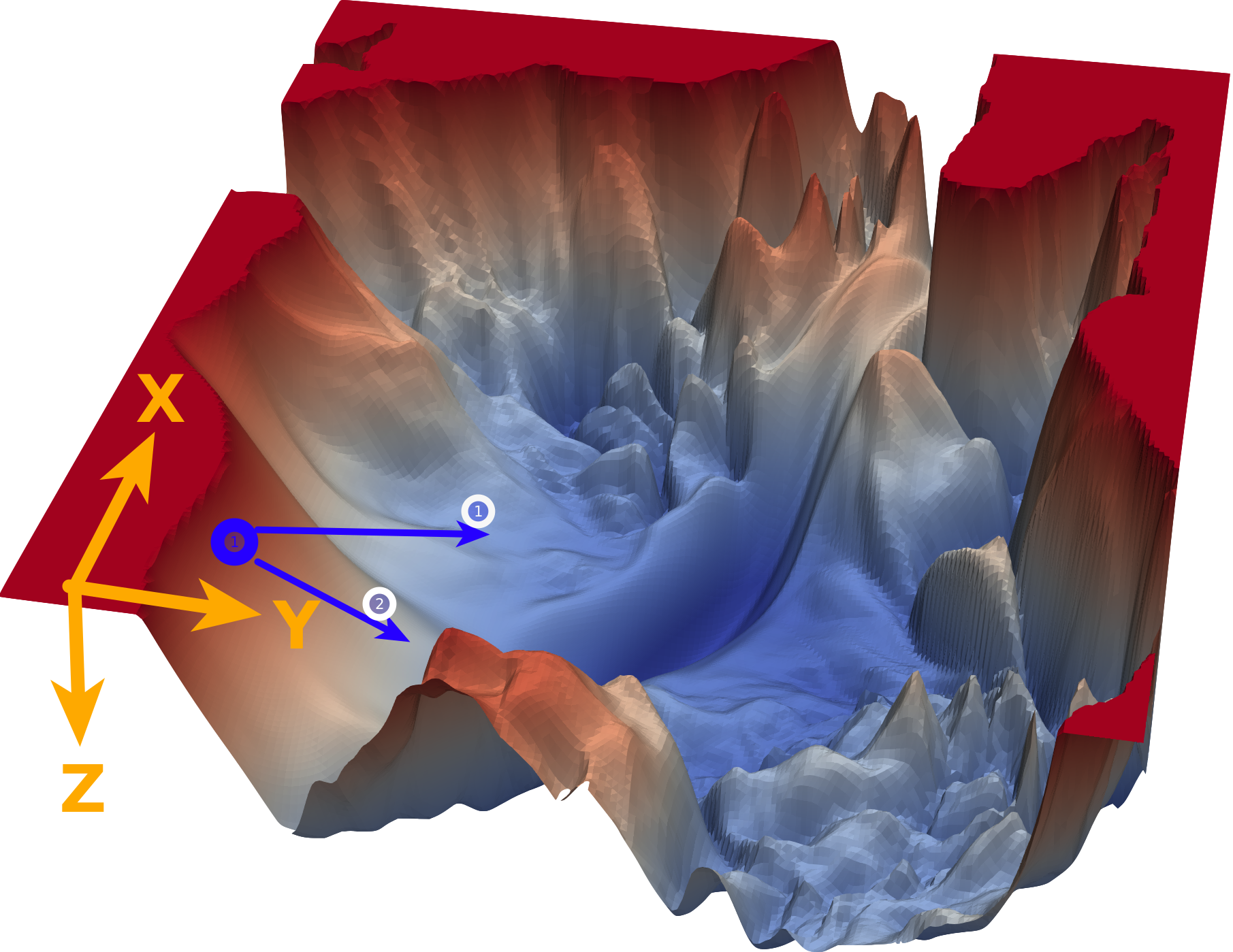
المصدر
لنستوضح الفكرة بشكل افضل، اذا نظرت إلى الرسم ستجد ان عند النقطة الزرقاء لدينا محور ال Z به انزلاق شديد و اذا اتبعنا التفاضل و كان للاتجاهات معدل تعلم متساوي اذا سوف نذهب في الإتجاه رقم 2 و هو يميل اكثر إلى محور ال Z لان الميل كبير في اتجاهه بالطبع على الرغم من ان الاتجاه رقم 1 اقرب إلى النقطة الأصغر و اسرع ايضا ولكن ما سنقوم بعمله هنا هو ان نخفض معدل التعلم في هذا المحور شديد الانزلاق عن باقي المحاور، اذا دعنا نرى كيف يتم ذلك رياضيا.
سوف نقوم بعريف متغير G و هو مجموع تربيع التفاضلات لكل اتجاه
$$ G_j^t = G_j^{t-1} + g_{tj}^2 $$
دعنا نستوضح المعادلة قليلا، هنا الرمز j يعبر عن الاتجاه بالتالي لكل اتجاه G مختلف و بالطبع g مختلف (g تعبر عن التفاضل في هذه اللحظة/المرة) ثم لدينا t و هي تعبر عن مرات التمرين.
اذا ما يحتويه G هو محصلة التفاضلات السابقة لهذا الاتجاه وسيصبح لدينا معلومة عن ماضي تفاضلات هذا الاتجاه و كلما كان الاتجاه منحدر اكثر (مثل اتجاه Z في مثالنا السابق) كلما كان مقدار ماضيه التفاضلي G اكبر بكثير.
و الان دعنا نرى كيف يمكننا تغيير معامل التعلم لكل اتجاه مع الاخذ في عين الاعتبار ماضيه التفاضلي
$$ w_j^{t} = w_j^{t-1} - \frac{\eta}{\sqrt{G_j^t + \epsilon}} g_{tj} $$
كما ترى هنا، كل وزن له تحديث خاص به وله معامل تعلم خاص به ايضا حيث يتم تخفيض معدل تعليمه بما هو قيمته
$$ \sqrt{G_j^t + \epsilon} $$
هنا المعامل ϵ يستخدم حتى لايكون المقام في عملية القسمة بصفر و تكون قيمته صغيرة جدا
و تلاحظ ايضا انه عند زيادة G لهذا الاتجاه فإن الخطوة التي يتخذها ستكون اصغر مع الوقت و قد تصل إلى ان تتوقف تماما وهذا احد عيوب هذا الطريقة في الحقيقة.
الانتشار المتوسط للجذر التربيعي (RMSprob - Root Mean Square Propagation)
هذه الطريقة تم تقديمها من خلال الدكتور جيفري هينتون في محاضرته السادسة في الكورس الذي يقدمه على منصة التعلم Coursera ولم تصدر به ورقة بحثية، لكن معظم الباحثين يشيروا اليه عن طريق رابط الكورس.
الفكرة هذه المرة هي ان نمنع الطريقة التكيفية من ان توقف التعلم بشكل كلي لان كما رأينا من قبل يمكن لمعدل التعلم ان يقل بشكل شديد حتى يختفي، لذلك هنا نقدم طريقة مختلفة لحساب التاريخ/السجل التفاضلي للمتغير عن طريق ان نقلل معدل التراكم كما سنرى في المعادلة الآتية.
$$ G_j^t = \alpha G_j^{t-1} + (1-\alpha) g_{tj}^2 $$
في غالب الامر تكون قيمة α 0.9 وبالتالي يكون الإعتماد على التاريخ التفاضلي بنسبة 0.9 و على القيمة الحالية للتفاضل بنسبة 0.1 و هكذا يقل معدل التراكم قليلا ونحافظ على ميزة التفاضل التكيفي اذ تظل معادلة تحديث الأوزان كما هي.
$$ w_j^{t} = w_j^{t-1} - \frac{\eta_t}{\sqrt{G_j^t + \epsilon}} g_{tj} $$
التقدير التكيفي اللحظي (Adam - Adaptive moment estimation)
حتى الآن تعرضنا لكيفية ضبط معدل التكيف على حدى و طريقة لضبط اتجاه التفاضل على حدى، الآن سنقوم بدمجهما معا في خوارزمية واحدة كما سنرى الآن.
تعتمد طريقة Adam على ان نستخدم معامل التعلم التكيفي الذي يقل تدريجيا في المواضع الاكثر انحدارا و ايضا ان نستخدم خاصية قوة الدفع وبالتالي نحصل على كلا الميزتين في طريقة واحدة، دعنا نستعرض المعادلات.
$$ m_j^t = \frac{\beta_1 m_j^{t-1} + (1-\beta_1) g_j^t}{1 - (\beta_1)^t} $$
$$ v_j^t = \frac{\beta_2 v_j^{t-1} + (1-\beta_2) g_j^t}{1 - (\beta_2)^t} $$
$$ w_j^t = w_j^{t-1} - \frac{\eta}{\sqrt{v_j^t}+ \epsilon} m_j^t $$
تجد في المعادلة الاخيرة ان الاوزان يتم تحديثها باستعواض m بدل من التفاضل العادي و كذلك يتم تخفيص معامل التعلم بمقدار المعامل v و اللذان يتم حسابهم باستخدام نفس المعادلة تقريبا، وستجد ان كلا المعادلتان في البسط هما عبارة عن احتفاظ بتاريخ الخطوات سواء m او v ولكن بمعامل β والذي يحدد ما إذا كنت تريد ان تعتمد على قيمة الماضي ام الحاضر اكثر
$$ \beta_1 m_j^{t-1} + (1-\beta_1) g_j^t $$
لاحظ هنا ان β مختلفة لكل معامل و غالبا ماتكون قيمتمها حوالي 0.9.
اذا الاختلاف في المقام الجديد (1-β) و هو في الحقيقة مستخدم لدفع العملية في خطواتها الأولى اذ انه مثلا في الخطوة الأولى عند t=1 وباستخدام β=0.9 سيكون قيمة المقام هي
$$ (1-\beta^t) = (1 - (0.9)^2) = (1-0.81) = 0.19 $$
اذا يتم قسمة المعامل m و v بقيمة 0.19 و هي كأنك ضاعفت مقداره 5 مرات
$$ \frac{1}{1-\beta^t} = \frac{1}{0.19} = 5.26 $$
وهكذا يتم دفع المعاملات في بداية التعلم لان قيمتهم في البداية ستكون قريبة من الصفر.
اشكال توضيحية
في الأشكال الآتية نرى مقارنة بين انواع مختلفة من خوارزميات النزول التدريجي و كيف ان بعضهم مناسب في احيان و بعضهم الاخر في احيان.
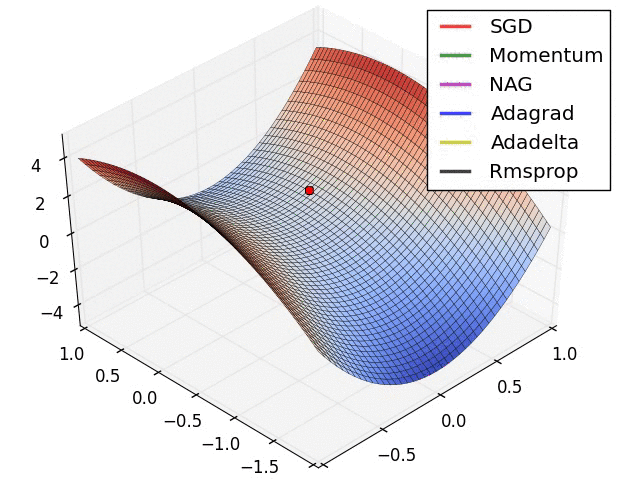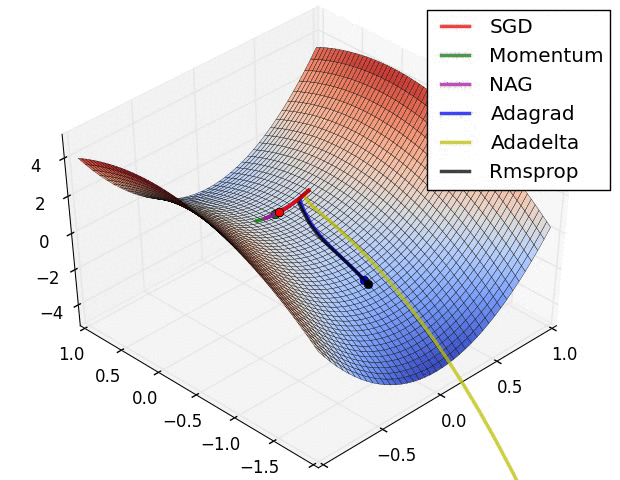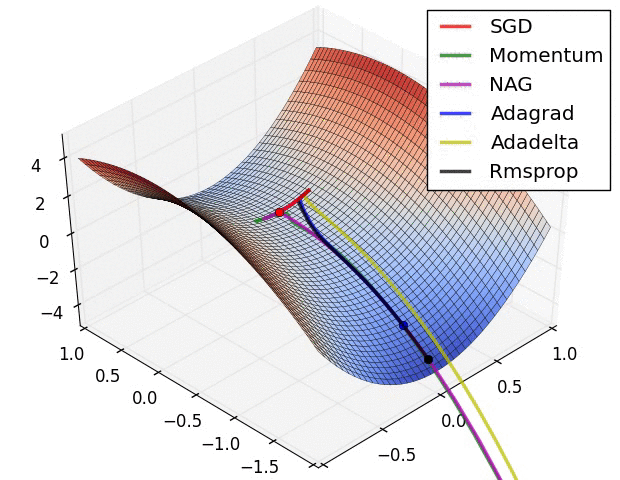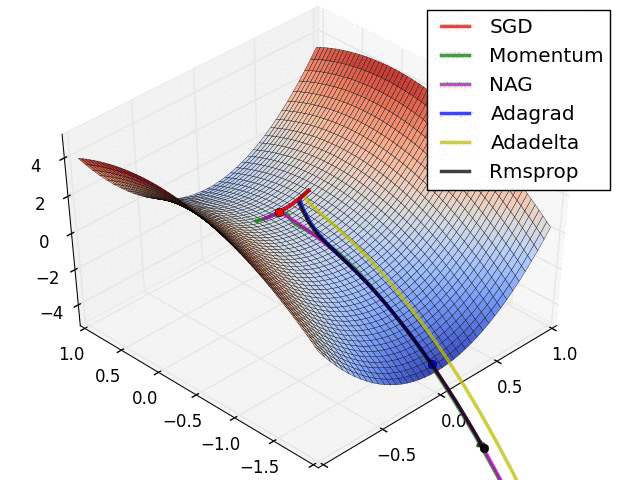
المصدر

المصدر

المصدر
لاحظ اختلاف تصرف الخوارزميات بإختلاف طبيعة الدالة المراد حلها.
يمكنك ايضا الاتطلاع على الكود المصدري للرسومات من خلال هذا الرابط
الاستنتاج
في هذا المقال تحدثنا عن انواع مختلفة من عائلة النزول التدريجي و اوجه الاختلاف بينهم وما الذي يميز كل واحد منهم.
لا يوجد طريقة افضل في المطلق من بينهم ولكن غالبا ما ستجد نفسك تقوم بالتجارب باستخدام اكثر من واحد ولكن من افضلهم Adam لهذا يمكنك ان تبدأ به و ترى أين سيقودك.
هناك انواع اخرى من Adam مثل Adamax و Adadelta و Nadam لم نقم بالتعرض لهم في مقالنا هنا ولكن فكرتهم ليست ببعيدة عما قمنا بشرحه، يمكنك الإطلاع عليهم من خلال
هذا المقال الرائع
في هذا المقال حاولت تبسيط بعض المصطلحات للغتنا العربية من اجل تسهيل عملية الشرح ولتبسيط المعلومة، في حالة اي خطأ املائي او اقتراح افضل للترجمة فأنا ارحب جدا بذلك يمكنك التعليق على المقال او مراسلتي لتعديل و تحسين المحتوى، ووفقنا الله وإياكم لما يحب ويرضى.
مصادر






















Comments