مقدمة
اغلبنا يتذكر مصطلح التباديل و التوافيق من المدرسة، غالبا نتذكر الاسم فقط و ننسى ما الفارق بينهم او غالبا ننساهم بالكلية، في هذا المقال سوف نقوم بتبسيط المعلومة حتى تصبح سهلة الاسترجاع فلا نضطر لحفظ المعادلات بعد الان لنعلم على سبيل المثال ما عدد كلمات المرور الممكنة في القفل الموجود بالصورة.
العدّ
العدّ هو اساس العمليات الحسابية، و هو ببساطة اننا نريد معرفة عدد معين من الاشياء دون ان نضطر ان نقوم بعدّهم واحد بواحد، و هذه العملية مهمة في كثير من التطبيقات العملية، ابسطها معرفة عدد الخطوات التي يحتاجها برنامج معين حتى يقوم بعمل مهمة ما، وكذلك لحساب المساحة التي يمكن ان تشغلها عملية معينة قبل تنفيذها.
فعلى سبيل المثال في هذه الصورة التي امامك هل يمكنك معرفة كم عدد الكرات دون ان تقوم بعّدهم واحدة تلو الاخرى ؟
بالتأكيد يمكنك ذلك عن طريق حساب عدد الصفوف و الاعمدة ثم حساب حاصل ضربهم ليكون الناتج هو عدد الكرات، وهكذا يكون ابسط مثال للعّد بدون الحاجة لعّد الامثلة واحدة تلو الاخرى ولكن هذه العملية لن تفلح في جميع الحالات، دعنا نرى كيف.
فلنفرض على سبيل المثال في موقعك الالكتروني لديك مجموعة فيديوهات و فئات مختلفة، مثل كوميديا، اكشن وهكذا، و لنقل ان الموقع يحتوي على 5 فيديوهات في فئة ما و 7 في فئة اخرى، فهل هذا يعني ان هناك 12 مقطع فيديو على موقعك ؟
ليس بالضرورة بالتأكيد لان الفيديو قد يقع في فئتين في نفس الوقت، مثل ان يكون كوميدي و اكشن مثلا، اذا لا يمكننا هنا ان نقوم بضرب عدد الفئات في الافلام كما فعلنا في مثال الكرات بالسابق ولكن نحتاج إلى حساب عدد الفيديوهات الموجودة فقط في الفئة الاولى و كذلك الفئة الثانية و نزيل الفيديوهات المكررة حتى لا نعدّها مرتين لعمل هذا نحتاج الى استخدام المجموعات، هل تتذكرها ؟
المجموعات
المجموعات هي عبارة عن مجموعة ارقام (او غير ارقام ولكن تركيزنا سيكون على الارقام)، لا يهم ترتيبهم ولا تكررارهم لان المجموعة هي الارقام المميزة فيمكننا القول بأن
\[\left \{1,1,1,2,3,3,4 \right \} = \left \{1,2,3,4 \right \}\]
هذا لان التكرار لا يهمنا هنا، وبالتالي يمكننا حساب تقاطع و اتحاد المجموعات، فان الاتحاد هو كل الارقام الموجودة في المجموعتين و التقاطع هي الارقام المشتركة كما تتذكر و يرمز لهم كما يلي.
\[A = \left \{1, 2, 3, 4, 5 \right \}\]
\[B = \left \{1, 3, 5, 7 \right \}\]
\[A \cap B = \left \{1, 3, 5 \right \} \rightarrow 1\]
\[A \cup B = \left \{1, 2, 3, 4, 5, 7 \right \} \rightarrow 2\]
نرى في المعادلة الاولى تقاطع المجموعتين و في المعادلة الثانية اتحادهما، يمكننا ايضا التعبير عن عدد العناصر في المجموعة كما يلي
\[A = \left \{1, 4, 6 \right \}\]
\[\left | A \right | = 3\]
اذا بالعودة إلى مثال الافلام في موقعك الذي تحدثنا عنه من قبل يمكننا صياغة المجموع بأنه مجموع الافلام في المجموعة الاولى و المجموعة الثانية طرح تقاطعهما كما في المعادلة الآتية
\[\left | A \cup B \right | = \left | A \right | + \left | B \right | - \left | A \cap B \right |\]
و يمكننا استخدام هذا القانون في العدّ بصورة عامة اذ اننا نقوم بعدّ كل مجموعة ثم نقوم بطرح التقاطع الذي يمثل الارقام التي قمنا بحسابها بالفعل مرة في مجموعة من المجموعات.
قاعدة الضرب
جميعنا نعلم قاعدة الضرب ولكن دعنا نتخيلها سويا، لنقل ان لدينا 3 طلاب و ان هناك 5 امتحانات، اذا كم درجة لدينا ؟
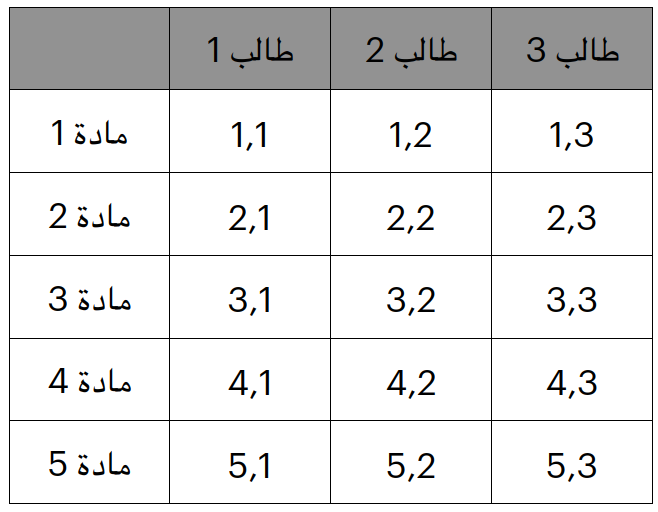
بالتأكيد النتيجة 15 لان هذا حاصل الضرب، لان لكل طالب هناك نتيجة في امتحان ما، اي ان مجموعة الطلاب المكونة من 3 كل طالب فيهم اصبح لديه مجموعة من الدرجات، و بالتالي اصبح لدينا ازواج من الطلاب و الدرجات كل زوج يمثل طالب ما و درجة امتحان ما، لهذا قمنا بحساب ضرب الطلاب و الدرجات!
كم كلمة سر يمكن تكوينها باستخدام القفل
باستخدام قاعدة الضرب كيف يمكننا حساب عدد كلمات السر التي يمكن تكوينها باستخدام هذا القفل ياترى؟، دعنا نرى كيف
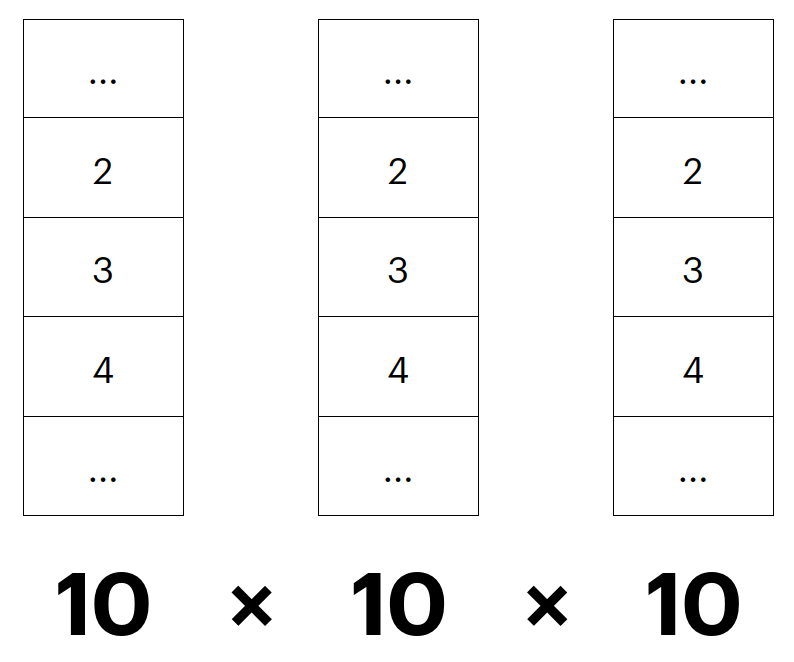
كما ترى، يمكننا في كل خانة ان نختار رقم من 0 الى 9، اذا عشرة ارقام في الخانة الاولى و مثلهم في الخانة الثانية و الثالثة و بهذا نقوم بحساب حاصل ضرب 10 × 10 × 10 و نحصل بالتالي على 1000 كلمة مرور يمكن تمثيلها بهذا القفل.
يمكن استخدام هذه الطريقة لحساب عدد العمليات التي يتطلبها برنامج لكسر كلمة مرورك على سبيل المثال، اذ انه يمكننا كما رأيت ان نستخدم هذه العملية بناءا على ما سبق و نقول انه يتطلب منك على اقصى تقدير 1000 عملية تخمين قبل ان تقوم بكسر شيفرة القفل بالأعلى هذا ان كان فقط يحتوي على ارقام، هل يمكنك التخمين الآن لماذا نستخدم ارقام و حروف ورموز ككلمة مرور ؟
يمكننا استنتاج قاعدة بسيطة هنا يمكن استخدامها في مواضع كثيرة و هي ما هي الاشكال التي يمكن الحصول عليها من متسلسلة من عدة رموز بمعلومية الرموز المتاحة، على سبيل المثال، في التعداد الثنائي (Binary numbering system) المستخدم في الدوائر الالكترونية، كم رقم يمكنك الحصول عليه اذا كان لديك 8 اماكن، و كل مكان يمكن ان يحمل قيمة من اثنين اما 0 او 1
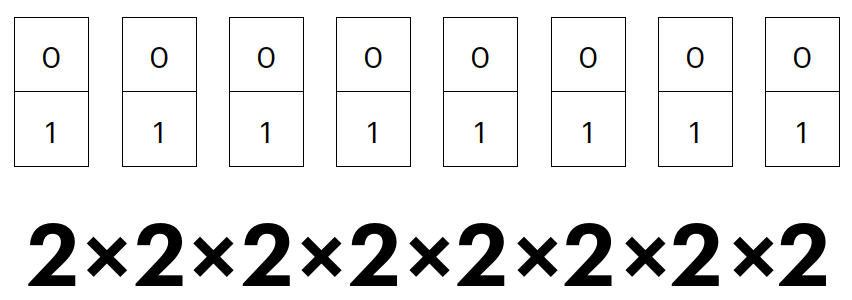
و هنا يمكننا استخدام القاعدة و هي ان مجموع الارقام التي يمكننا الحصول عليها هي عدد الرموز الممكنة أُس عدد الاماكن المتاحة، بالتالي في مثالنا هنا سيكون محصلة الارقام المتاحة هي
\[2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 = 2^8 = 256\]
مجموعات بشروط
لننظر إلى مشكلة اخرى اكثر تعقديا ونرى كيف يمكن حلها باستخدام قاعدة الضرب و بدون الحاجة إلى عد جميع الاحتمالات
من بين الارقام 0 و 9999، كم رقم يمكننا الحصول عليه يحتوي على الرقم 7 مرة واحدة فقط به مثل 1117 و ليس مثلا 1717 لابد من وجود 7 مرة واحدة فقط ؟
لنحل هذه المسألة دعنا نفكر بها بنفس الطرق السابقة، في البداية يمكننا استخدام الرقم 7 في الخانة الاولى و هذا يعطي جميع الخانات الاخرى الاختيار بين اي رقم ماعدا ال 7 هكذا يصبح لدينا 9 اختيارات من 0 إلى 6 و 8 و 9، وبهذا يصبح مجموع الارقام الممكنة مع وجود 7 واحدة فقط في البداية هي
\[9 \times 9 \times 9 = 729\]
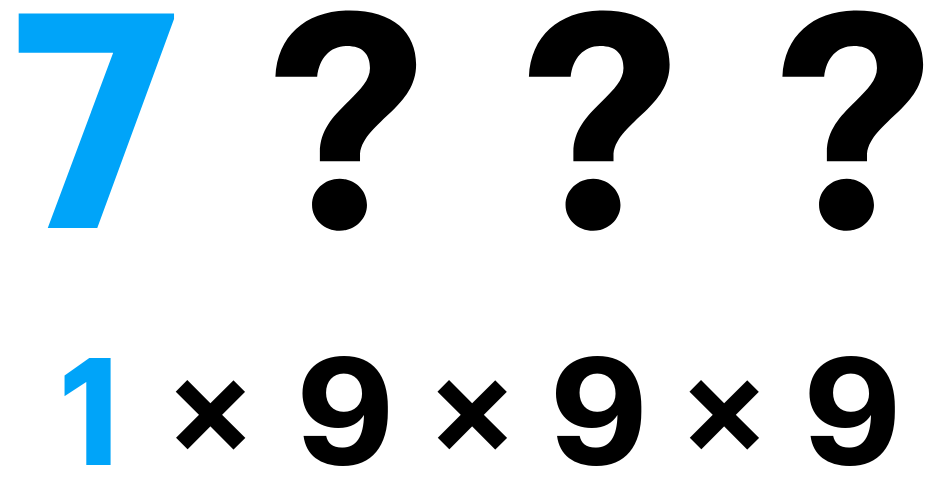
اذا بهذا الشكل فقط يمكننا الحصول على 729 رقم، ولكن الرقم 7 يمكنه ان يكون في اي مكان من ال 4 اماكن، وفي جميع الحالات سيكون مجموع الارقام الممكنة هي 729، اذا فإن محصلة الارقام التي يمكننا الحصول عليها و تحتوي الرقم 7 مرة واحدة فقط هي.
\[729 \times 4 = 2916\]
التباديل Permutations
والآن لموضوعنا الرئيسي و هو التباديل، ولكن ما هي التباديل على اية حال؟، دعنا نرى مثال على التباديل لنفهم تعريفها بشكل افضل.
فلنفرض ان اسمك هو "علي"، كم كلمة يمكننا كتابتها باستخدام حروف اسمك بدون استخدام نفس الحرف مرتين ؟
الكلمات على سبيل المثال "يلع" او "يعل" وهكذا، اذا كم كلمة يمكنك الحصول عليها ؟
الكلمات على سبيل المثال "يلع" او "يعل" وهكذا، اذا كم كلمة يمكنك الحصول عليها ؟
في هذا المثال اسمك يتكون من 3 احرف، اذا في اول حرف لديك حرية الاختيار بين ايا منهم، اذا اول حرف يحمل 3 احتملات {ع, ل, ي}، ثم نأتي للحرف الثاني، سيكون امامك احتمالين فقط من الحروف اذ ان الحرف الذي تم اختياره من قبل المكان الاول لا يمكن اختياره الان لذا لديك فقط اختيارين، وهذا يترك اختيار واحد فقط للمكان الاخير و هذا يعطينا عدد من الكلمات يساوي 3 × 2 × 1 و بهذا يمكننا الحصول على 6 كلمات باستخدام حروف اسمك، دعنا نرى المثال بصورة اوضح.
لنقل ان في المكان الاول اخترنا الحرف "ي" اذا في المكان الثاني لدينا فقط الحروف {ع, ل} لنختار منهم، و اذا اخترنا الحرف "ع" على سبيل المثال سيتبقى للمكان الاخير حرف واحد فقط للاختيار و هو حرف "ل"
يمكننا تعميم هذه الحالة كما يلي، في حالة ان لديك عدد رموز n للاختيار منهم (على سبيل المثال الحروف الابجدية مثلا) و نريد تكون مجموعة طولها k رمز (مثل ان تكون الكلمة من 3 احرف مثلا) فإن مجموع الكلمات التي يمكنك الحصول عليها هو
\[n \times (n-1) \times (n-2) ... (n-k+1) = \frac{n!}{(n-k)!}\]
لاحظ ان في حالة ان n=k سيكون المقام بصفر، ولكن نفرض ان مضروب 0 = 1 وبهذا اذا كانت n=k فان مجموع التباديل هو n!
لنرى مثال على هذا، اذا كان لديك 5 كتب، وتريد ان تعرف كم طريقة يمكنك ترتيبهم بها على ارفف مكتبتك، كم طريقة يمكنك ترتيبهم بها ؟
لنرى مثال على هذا، اذا كان لديك 5 كتب، وتريد ان تعرف كم طريقة يمكنك ترتيبهم بها على ارفف مكتبتك، كم طريقة يمكنك ترتيبهم بها ؟
لتوضيح المثال كما فعلنا من قبل، في اول مكان يمكننا الاختيار من الكتب كلها، في ثاني مكان سنختار من الكتب كلها ماعدا الذي قمنا بإختياره، وهكذا مع كل خطوة تقل اختياراتك حتى تنهي الكتب و بهذا يصبح عدد الطرق التي يمكنك ترتيب كتبك بها هي
\[n \times (n-1) \times (n-2) ...(n-n+1) = n! = 5! = 120\]
اذا يمكنك ترتيب الكتب ب 120 طريقة كما ترى
التوافيق Combinations
لنقل ان لدينا 5 كرات و نريد ان نعرف كم مجموعة يمكننا تكوينها باستخدام 3 كرات بدون تكرار ايا من المجموعات، دعنا نرى تفاصيل هذا العملية
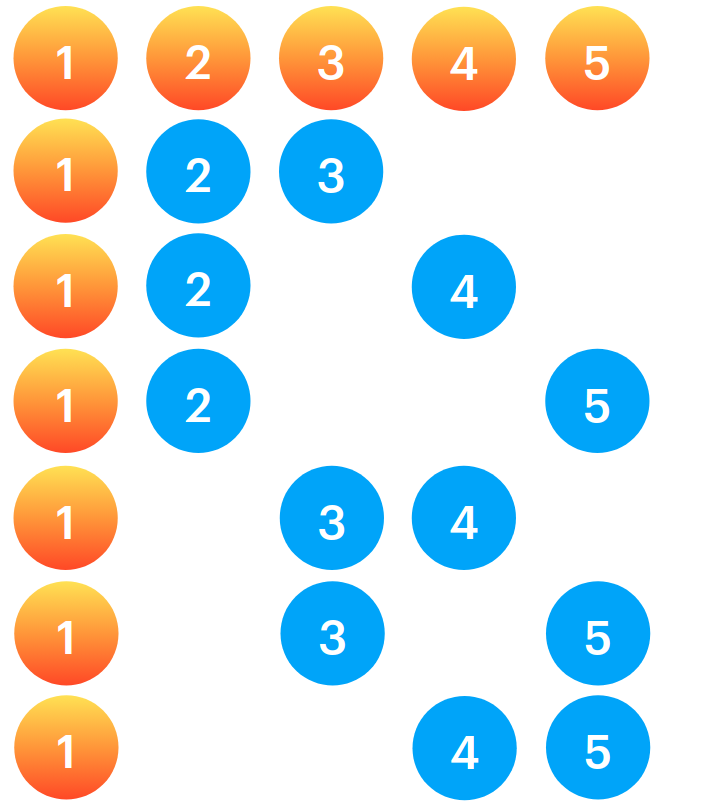
هنا يمكنك تن ترى اننا قمنا بتثبيت الكرة الاولى و اخترنا على اساسها باقي الكرات، لنرى عندما نقوم بتثبيت الكرة الثانية ماذا سيحدث
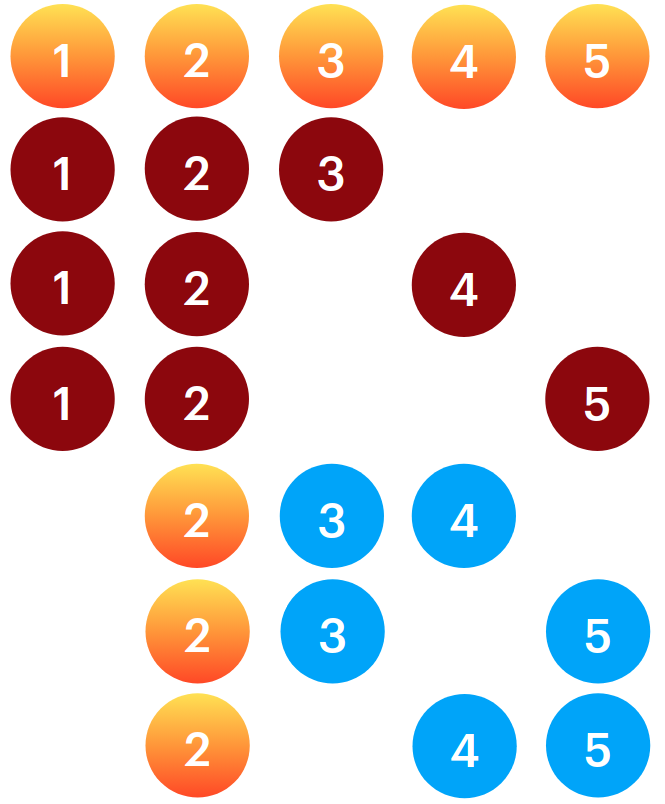
يمكنك ان ترى هناك عدة مجموعات متكررة مثل {1, 2, 3} و ايضا {1, 2, 4} بالتالي اذا قمنا بعمل حساباتنا مثل التبادل سوف نجد ان هناك العديد من التكرار بها، ونحن نريد حساب فقط العمليات المميزة، اذا كيف يمكننا ذلك ؟
في مثالنا السابق اردنا اختيار مجموعات مكونة من 3 كرات من اصل 5 كرات، و اذا قمنا بحساب مجموع عدد المجموعات التي يمكننا تكوينها بما في ذلك مرات التكرار سنجد ان مجموعهم هو
\[5 \times (5-1) \times (5-2) = \frac{5!}{(5-3)!} = 60\]
والان دعنا نحسب عدد مرات التكرار التي يمكن ان تظهر في مجموعاتنا، بما ان كل مجموعة تتكون من 3 كرات، اذا فيمكننا تحويلها لنفس نمط عدد الكلمات التي يمكنك تكوينها باستخدام حروف اسم "علي" هذا لان الكرات مثلا {1, 2, 3} يمكن ايضا ان تظهر بشكل {2, 1, 3} وبهذا يصبح لديك نفس المجموعة ولكن فقط ترتيبها مختلف، اذا يمكننا ان نحسب كم شكل يمكن تكوينه من كل مجموعة و نقوم بقسمة التباديل عليه و بالتالي سنحصل على المجموعات و لكن بدون المجموعات المكررة ونحصل على المعادلة الآتية لحساب التوافيق
\[\binom{n}{k} = \frac{n!}{k! (n-k)!}\]
لاحظ ان الاقواس تعني كم مجموعة مميزة طولها k يمكننا ان نحصل عليها من مجموعة مكونة من n عنصر.
بتطبيق هذه العملية على مثالنا يمكننا ان نحصل على عدد المجموعات المميزة و هو كما يلي
\[\binom{5}{3} = \frac{5!}{3! (5-3)!} = 10\]
اذا يمكننا فقط الحصول على 10 مجموعات مميزة من الكرات الخمس اذا كان طول المجموعة 3
كيفية استخدام التباديل و التوافيق في لغة البايثون
الان دعنا نرى كيف يمكننا ان نستخدم هذه القواعد في لغة ال Python للحصول على تباديل و توافيق من مجموعة ارقام list على سبيل المثال
from itertools import permutations
numbers = [1, 2, 3, 4, 5]
my_permutations = permutations(numbers)
for perm in my_permutations:
print(perm)
>>> [(1, 2, 3, 4, 5),
>>> (1, 2, 3, 5, 4),
>>> (1, 2, 4, 3, 5),
>>> (1, 2, 4, 5, 3),
>>> (1, 2, 5, 3, 4),
>>> (1, 2, 5, 4, 3),
>>> ...
يمكنك ايضا الحصول على جميع التباديل مرة واحدة بدون الحاجة لاستخدام for loop كما يلي
from itertools import permutations
numbers = [1, 2, 3, 4, 5]
my_permutations = list(permutations(numbers))
print(len(my_permutations))
>>> 120
و الان لنرى كيف يمكننا ان نحصل على التوافيق بمثال الكرات الخمس الذي استخدمناه سابقا
from itertools import combinations
numbers = [1, 2, 3, 4, 5]
# 3 here represents K in our example
my_combs = combinations(numbers, 3)
for comb in my_combs:
print(comb)
>>> [(1, 2, 3),
>>> (1, 2, 4),
>>> (1, 2, 5),
>>> (1, 3, 4),
>>> (1, 3, 5),
>>> (1, 4, 5),
>>> (2, 3, 4),
>>> (2, 3, 5),
>>> (2, 4, 5),
>>> (3, 4, 5)]
على غرار المثال السابق يمكننا ايضا الحصول عليهم بشكل مباشر
from itertools import combinations
numbers = [1, 2, 3, 4, 5]
# 3 here represents K in our example
my_combs = list(combinations(numbers, 3))
print(len(my_combs))
>>> 10
خاتمة
في هذا المقال تحدثنا عن التباديل و التوافيق و كيف يمكننا ان نسترجع الفارق بينهم وكيفية حسابهم دون الحاجة الى حفظ المعادلة لان ببساطة يمكنك استرجاع المعلومة و طريقة فهمك لها وبالتالي لا يوجد حاجة لحفظ المعادلات بعد الان هنا.
تحدثنا عن كيف ان العدّ هو ابسط ولكن من اهم العمليات في الرياضيات و استخداماته كثيرة جدا، و كيف ان التباديل هي جميع الاشكال التي يمكنك الحصول عليها من مجموعة رموز مع امكانية تبديلهم و التوافيق هي التباديل ولكن مع مراعاة عدم تكرار المجموعات بها.
تحدثنا عن كيف ان العدّ هو ابسط ولكن من اهم العمليات في الرياضيات و استخداماته كثيرة جدا، و كيف ان التباديل هي جميع الاشكال التي يمكنك الحصول عليها من مجموعة رموز مع امكانية تبديلهم و التوافيق هي التباديل ولكن مع مراعاة عدم تكرار المجموعات بها.
في هذا المقال حاولت تبسيط بعض المصطلحات للغتنا العربية من اجل تسهيل عملية الشرح ولتبسيط المعلومة، في حالة اي خطأ املائي او اقتراح افضل للترجمة فأنا ارحب جدا بذلك يمكنك التعليق على المقال او مراسلتي لتعديل و تحسين المحتوى، ووفقنا الله وإياكم لما يحب ويرضى.
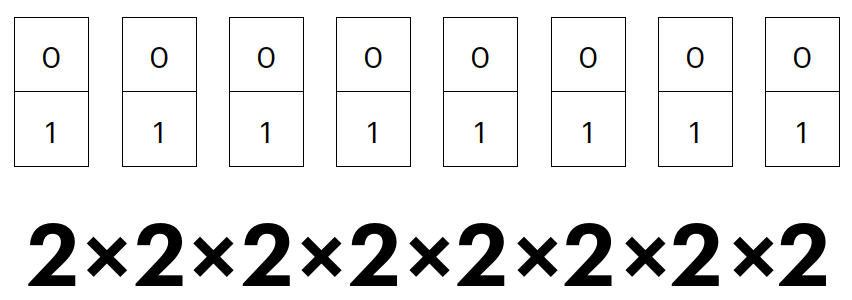
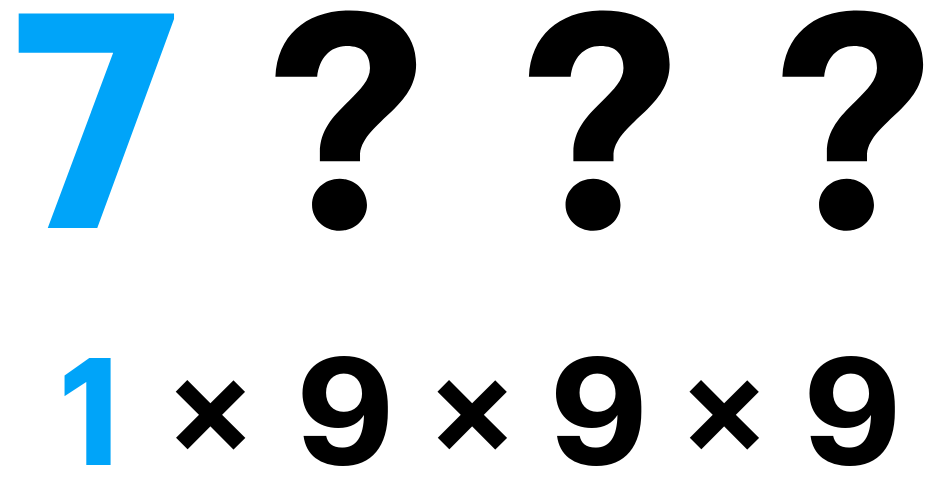
Comments