مقدمة في علم الآلة

مجال تعلم الآلة او (machine learning) هو احد فروع الذكاء الاصطناعي و يشتمل بداخله علم التعلم العميق (deep learning)

و عرفه العالم آرثر سامويل

ان تعطي اجهزة الكمبيوتر القدرة على التعلم بدون ان تتم برمجتها بشكل صريح
المصدر

لتوضيح هذا العنوان بشكل افضل، لنستعرض الفرق بين البرمجة الحرفية و تعليم الآلة بشكل مبسط

البرمجة التقليدية (الحرفية)

لنقل على سبيل المثال اننا نود ان نميز بين اذا ما كان في الصورة قطة ام لا المصدر ففي حالة البرمجة التقليدية سوف نقوم بوضع جميع القواعد التي تحتاجها الآلة حتى تميز هذا القطة مثل ان اذنها يجب ان تكون مثلثة الشكل قليلا و ان وجهها يجب ان يكون دائريا نوعا ما و ايضا ان تحتوى على فراء، وهكذا إلى اخر القواعد التي يمكنك كتابتها
وفي حالة ان احد هذه القواعد لم تماثل ماقمت بتعريفه لن نتمكن من ان نتعرف على القطة في الصورة للاسف.

if ear is triangle:
  if face is circular:
    if object has furr:
      if image is cute:
          "it's a cat!"

بالطبع يمكنك الملاحظة ان هنا لن نتمكن من تغطية جميع المواصفات التي تميز القط، ناهيك عن اختلاف القرب او البعد عن الصورة على سبيل المثال او تغيير مكان القطة في الصورة او حتى طريقة تحديد هذه المواصفات
بالتالي هذه ليست الطريقة الافضل في هذه المهمة، لذا تعالى معي نستعرض الطريقة الاخرى و هي باستخدام تعليم الآلة

طريقة تعليم الآلة (التعلم من البيانات)

في هذه الطريقة نعتمد بالاساس على ان نوفر صور مختلفة لقطط و اي شئ غير القطط و نترك الامر لما سوف ندعوه نموذج كي يتعلم ماهية القط و كيف يمكنه تمييزه عن غيرها من الاشياء.
بالطبع هذه الطريقة تعتمد على ان يتوفر صور عدة للقطط وكذلك لغير القطط حتى يتمكن نوذجنا من معرفة القط من غيره و من هذا المنطلق تنشأ الحاجة الى كثير من البيانات حتى نتمكن من عمل نوذج قوي يمكنه التمييز، و توفر البيانات بكثرة في العقد الاخير سمح بتقدم هائل في مجال تعلم الآلة والذكاء الصناعي بشكل عام.

cats = [cat1, cat2, cat3, ...]
machine_learning_model.learn_from(cats)
machine_learning_model.predict(new_image)

حسنا عرفنا الآن الفرق الاساسي بين التعلم من البيانات و الطرق المعتمدة على البيانات التي يطلق عليها (data driven approaches) وكذلك الطرق التي تعتمد على ان نعطيها القواعد التي تم تصميمها يدويا (rule based approaches).
ولكن كيف للآلة ان تتعلم هكذا صفات؟ و ان تفهم النمط المتواجد في البيانات و بناءا عليه تمييز البيانات الجديدة التي لم يراها من قبل؟
لنفهم هذا دعنا ننظر الى مثال بسيط في هذا الشأن

استخراج النمط من البيانات

لنقل على سبيل المثال ان لديك منزل تريد ان تبيعه، ولا تعرف اي سعر قد يكون مناسب لك و لكنك تعلم ان اخر 3 بيوت تم بيعهم في المنطقة المحيطة لك كانت اسعارهم و مواصفاتهم كالاتى

الطابق الواقع فيه المنزل	مساحة المنزل	سعر البيع
الثالث	300	9300
الاول	250	7600
الخامس	100	800

و لديك مواصفات منزلك و الذي يقع في الطابق الثاني و مساحته 220 اذا ما هو السعر المناسب لمنزلك؟
بالطبع يمكننا ان نقوم بتحويل هذه المسألة إلى معادلات في متغيريين كما يلي
اذا اعتبرنا ان الطابق هو متغير X و ان المساحة هي متغير Y اذا يمكننا ان نصف اول منزلين كما يلي

\[3X + 300Y = 9300\] \[1X + 250Y = 7600\]

نستطيع حل هاتان المعادلتان سويا و استخراج X بدلالة Y ثم ايجاد قيمتهما سويا كما يلي

\[\because X = 7600 - 250 Y\] \[\therefore 3 (7600 - 250 Y) + 300 Y = 9300\] \[\therefore Y = 30\] \[\therefore X = (7600 - 250 * 30) = 100\]

و هكذا يمكننا ان نحسب ثمن المنزل الذي نريد ان نبيعه كالتالي

\[100 * 2 + 30 * 220 = 6800\]

هنا يمكنك تفسير قيمة X و Y على انهم اهمية الطابق الذي تقع .فيه الشقة و مساحتها على الترتيب

بالتالي هنا نرى ان اهمية الطابق قيمتها 100 و اهمية المساحة قيمتها 30.

ما فعلناه للتو هو تخصيص ما يسمى اوزان او(weights) للمتغيرات او الخصائص التي لدينا وهي الطابق و المساحة، وهذا هو المبدأ الأساسي الذي تقوم عليه عملية التعلم اذ نقوم بتخصيص وزن لكل متغير يصف البيت او ما يسمى (feature) و نقوم بحساب هذه الاوزان.
دعنا نرى كيف تقوم الآلة بعمل هذه العملية.

كيفية حساب الاوزان

لنكمل على المثال السابق، دعنا نقول ان المنزل يتم توصيفه بعدد من المتغيرات N، مثل مساحته، الطابق، المحافظة ، وهكذا.
و ان لدينا عدد m من المنازل وهي التي سنقوم من خلالها بحساب الاوزان الخاصة بكل متغير وسوف نرمز لهذه الاوزان برمز W اذا دعنا نرى المعادلة الخاصة بالمنزل رقم i والذي سعره Y

\[w_1 x_{1}^{(i)} + w_2 x_{2}^{(i)} + w_3 x_{3}^{(i)} + .... + w_n x_{n}^{(i)} = y^{(i)}\]

في هذه المعادلة يمكنك ان ترى ان كل خاصية في المنزل مخصص لها وزن محدد و ان تكلفة المنزل هي محصلة ضرب كل وزن في الخاصية المحدد لها، وطبعا لن يمكننا حساب هذه الاوزان عن طريق معادلة واحدة، وانما عدد m من المعادلات، و الذي هو عدد المنازل كما تذكر

\[w_1 x_{1}^{(1)} + w_2 x_{2}^{(1)} + w_3 x_{3}^{(1)} + .... + w_n x_{n}^{(1)} = y^{(1)}\] \[w_1 x_{1}^{(2)} + w_2 x_{2}^{(2)} + w_3 x_{3}^{(2)} + .... + w_n x_{n}^{(2)} = y^{(2)}\] \[...\] \[w_1 x_{1}^{(m)} + w_2 x_{2}^{(m)} + w_3 x_{3}^{(m)} + .... + w_n x_{n}^{(m)} = y^{(m)}\]

الآن كيف نقوم بحساب هذه المتغيرات؟، بالطبع يمكننا حسابه بنفس الطريقة التي قمنا بها بالاعلى، إلا ان هذه الطريقة سوف تكون مكلفة حسابيا بشكل كبير و ربما نتعرض في مقال اخر لمدى تعقيدها، ولكن لحسن الحظ هناك طريقة اخرى اكثر فعالية و اسرع في حسابها و هي النزول التدريجي او (gradient descent)
لنفهم هذه الطريقة دعنا نقوم بتعريف المشكلة بشكل اخر.

النزول التدريجي (gradient descent)

توصيف المشكلة

دعنا الان نعبر عن المشكلة بشكل افضل، كما هو موضح بالشكل ادناه.

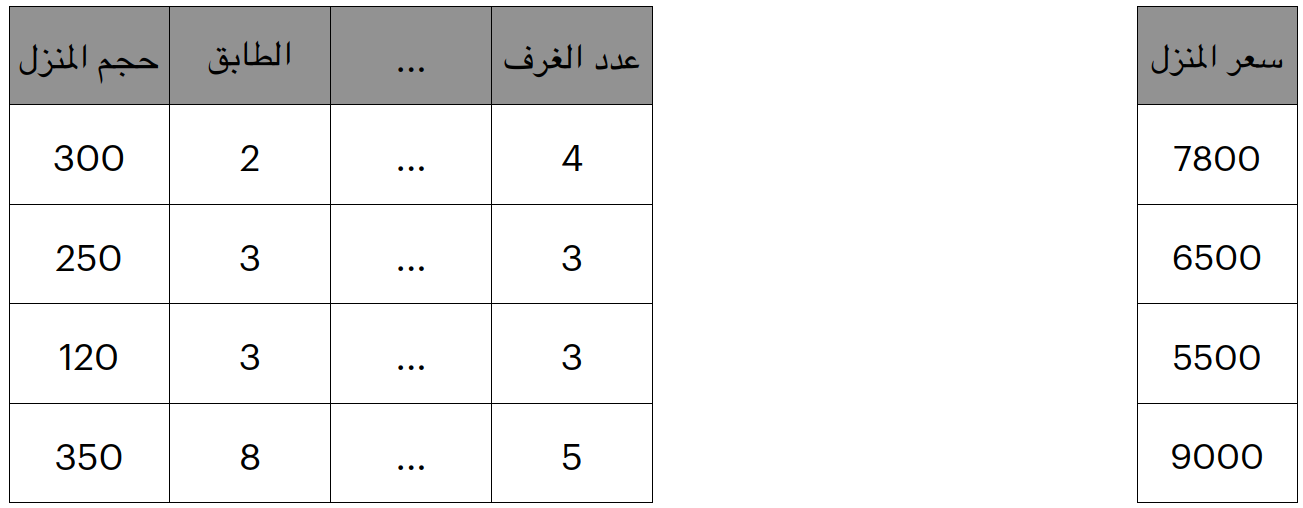
سنتبع طريقة لذيذة هنا، دعنا نخمن ما هي افضل قيمة للاوزان و لنقل مثلا صفر و نرى كيف سنتكون النتيجة؟

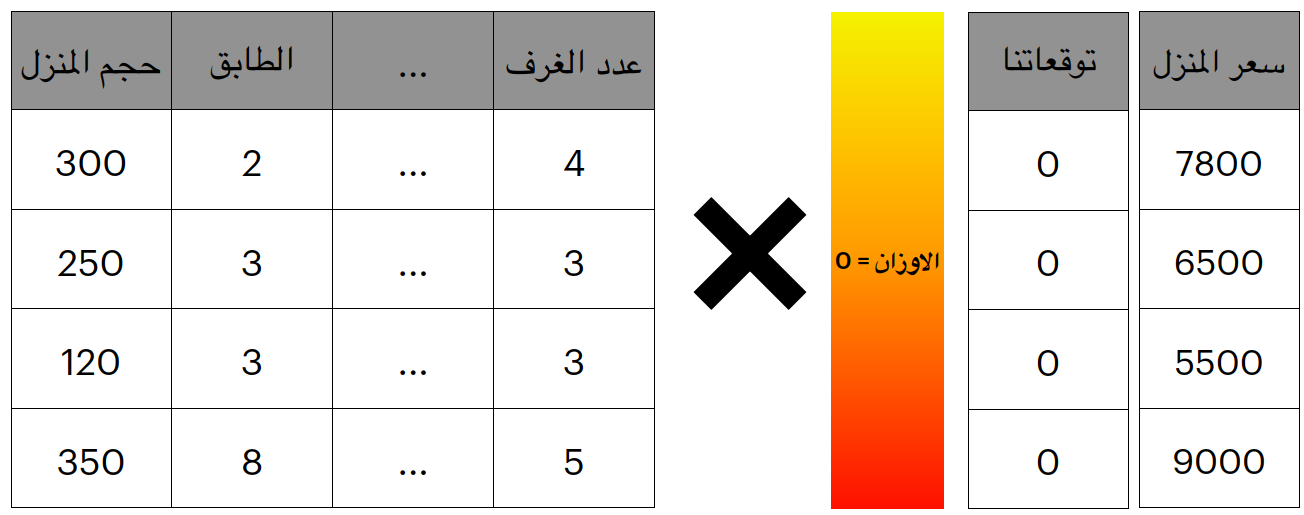
كما يمكنك ان ترى، جميع المنازل الان صار سعرها صفر لان ببساطة كل منزل يتم حساب سعره كما يلي

\[0 * x_{1}^{(i)} + 0 * x_{2}^{(i)} + 0 * x_{3}^{(i)} + .... + 0 x_{n}^{(i)} = \hat{y} = 0\]

الرمز Y^ يعبر عن التوقعات

اذا صفر ليس القيمة الصحيحة للاوزان و نحتاج الى تغيرها، اذا ما الرقم الذي نحتاجه؟ و ما هو الرقم الافضل لكل متغير؟
في البداية دعنا نرى مدى الخطأ الذي ادى اليه الصفر ثم ننظر كيف يمكننا ان نقلل هذا الخطأ تدريجيا اذا، ولحساب هذا الخطأ سوف نستخدم الفرق بين توقعنا والسعر الصحيح ولاننا يمكن في مرحلة ما ان يصبح لدينا قيم سالبة سوف نرفع القيمة للأس الثاني كما هو موضح بالمعادلة ادناه

\[Error^{i} = ( \hat{y}^{i} - y^{i})^{2}\]

هذه هي معادلة الخطأ لنقطة واحدة، فمثلا في حالتنا هذه يصبح الخطأ في أول مثال قيمته كالتالي

\[Error^{1} = ( \hat{y}^{1} - y^{1})^{2} = (0 - 7800)^{2} = 60840000\]

و هكذا نحتاج لمعرفة الخطا على مستوى جميع المنازل التي لدينا والتي عددها m كما قلنا من قبل، لذلك سوف نقوم بحساب حاصل جمع كل الاخطاء على مستوى المنازل كلها و كما ترى لان الرقم كبير نسبيا سوف نقوم بأخذ المتوسط لهذه المحصلة ليصبح الرقم اقل قليلا ولكن مازال معبرا عن الخطأ فقط ابسط في الحسابات

\[Error = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{i} - y^{i})^2\]

الان اصبح لديك معادلة تعبر عن مدى الخطأ في توقعاتنا ومدى بعد توقعاتنا عن الصواب بالتالي كلما قلت هذه المعادلة كقيمة كلما كانت توقعاتنا صحيحة لان عندما تكون التوقعات سليمة يصبح $$ \hat{Y} - Y = 0$$و بالتالي سيصبح الخطأ الكلي صفر
اذا هدفنا الان هو ان نصل لطريقة تمكننا من تقليل قيمة هذه المعادلة وهنا يأتي دور التفاضل اذا كنت تذكره، ان لم تكن تذكره فسوف نتذكره سويا في الفقرة التالية

تطبيق التفاضل في تعلم الآلة

تفاضل دالة ما هو معدل تغير قيمتها بالنسبة لمتغير من متغيراتها فعلى سبيل المثال في الدالة الآتية عندما نقوم بحساب معدل تغير Y بالنسبة ل X نحن نقوم بطرح سؤال و هو اذا قمنا بتغيير قيمة X كم ستتأثر Y و ايضا يمكننا طرح سؤال اخر و هو اين اتجاه زيادة قيمة Y بالنسبة ل X بمعنى، هل نحتاج ان نرفع قيمة X ام نخفضها حتى تزيد قيمة Y

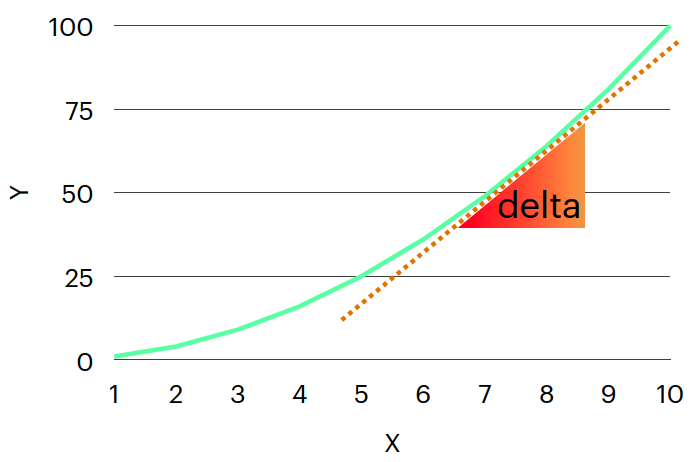
$$ y = x^2 $$ اذا كنت تتذكر قواعد التفاضل فانك ستتذكر ان تفاضل هذه الدالة هو 2x $$ \frac{d}{dx} = 2x $$ و قد تلاحظ هنا ان التفاضل يحتوي على متغير، اي ان قيمة التفاضل تختلف بختلاف مكانك في الدالة و اذا قمنا باختبار ذلك في موضعين مختلفين في الدالة على سبيل المثال سنجد ان قيمة التفاضل بالفعل تختلف لنرى كيف

التفاضل يمكن حسابه عن طريق الميل او ال (slope) بين نقطتين في الدالة و سوف نقوم بحساب التغيير بناءا على ذلك اولا بين نقطتين هما

(7, 49), (8, 64)

$$ Slope = \frac{y_1-y_2}{x_1-x_2} = \frac{49-64}{7-8} = 15 $$ اذا معدل التغيير هنا هو 15 و ايضا كما تلاحظ 2x حيث x = 7.5
و الان لنرى قيمة التفاضل بين نقطتين اخرتيين (1, 1), (2, 4)

$$ Slope = \frac{y_1-y_2}{x_1-x_2} = \frac{1-4}{1-2} = 3 $$ سنجد ان معدل التغير اختلف عن المكان السابق و قيمته هنا 3

نسنتنج مما سبق ان معدل التغير في الدالة يختلف من مكان لاخر بها و لذلك يوجد متغير x في معادلة التفاضل و ايضا نستطيع ان نرى مما سبق ان التفاضل عند النقتطين كان قيمته موجبة اي ان مع زيادة X سوف تزداد قيمة Y على عكس اذا ما حسبنا التفاضل بين نقطتين سالبتين مثلا

(-2, -4) (-1, -1)

$$ Slope = \frac{y_1-y_2}{x_1-x_2} = \frac{-4+1}{-2+1} = -3 $$ نجد في الجزء السالب من هذه الدالة ان زيادة X سوف تقلل من قيمة Y ولهذا يظهر التفاضل بقيمة سالبة

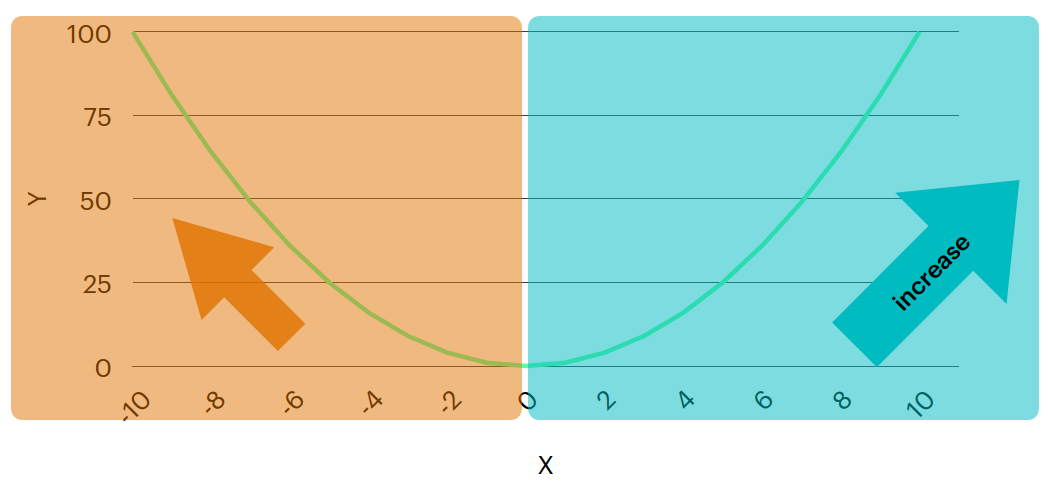
اذا التفاضل يمكنه اخبارنا اين هو اتجاه زيادة الدالة بالنسبة لمتغير معين وبالتالي فإن عكس هذا الاتجاه سيكون هو اتجاه النقصان، اذا عند اي نقطة في الدالة اذا فاضلناها سنعلم اي اتجاه نحتاج ان نسير اليه لتقليل قيمة هذه الدالة وهذا ايضا ليس لمتغير واحد وانما لاكثر متغير اذ انه يمكنك ان تفاضل الدالة لاكثر من متغير و سوف تحصل على اتجاه الزيادة لكل متغير، اذا كنت تتساءل عن شكل الدالة في حالة ان بها اكثر من متغيرين فهي كالشكل الآتي

المصدر

في هذه الحالة نقوم بحساب التفاضل بالنسبة لكل متغير على حدى و نرى لكل متغير على حدى ما علاقته بالدالة بشكل عام وما التغيير الذي نحتاج ان نقوم به حتى تزداد الدالة بشكل عام فبالتالي نستطيع ان نوجد اتجاه نقصانها

كيفية استخدام التفاضل في تحسين توقعاتنا

الآن لدينا مجموعة من الاوزان (weights) التي خصصناها لمجموعة من ال (features) او الخصائص التي من المفترض ان من خلالها سنستطيع ان نستنتج سعر اي منزل جديد، ولدينا ايضا معادلة الخطا التي تقيم مدى قربنا او بعدنا عن الصواب و الذي هو بدوره تقييم للاوزان نفسها كما رأينا في مثال الصفر بالأعلى $$ Error = \frac{1}{2m} \sum_{i=1}^{m} (\hat{y}^{i} - y^{i})^2 $$ وبالنظر إلى المعادلة التي استنتجنا منها Y^ سنجد انها معادلة في الاوزان بالاساس $$ w_1 x_{1}^{(i)} + w_2 x_{2}^{(i)} + w_3 x_{3}^{(i)} + .... + w_n x_{n}^{(i)} = y^{(i)} $$ واذا عبرنا عن الاوزان كلها ب W و الخصائص كلها ب X يمكننا التعبير عن نوذجنا كالتالي $$ W*X = \hat{Y} $$ بالتالي معادلة الخطأ تصبح $$ Error = \frac{1}{2m} \sum_{i}^{m} ( W*x^{i} - y^{i})^2 $$ الان يمكننا استخدام التفاضل لنوجد اتجاه الزيادة لهذه المعادلة و بالتالي عكسه سوف يكون اتجاه النقصان و بالتالي يمكننا ان نعدل كل وزن ليسير في اتجاه النقصان الخاص بالدالة. $$ \frac{d}{dW} Error = \frac{1}{m} \sum_{i}^{m} (W*x^{i} - y^{i})x^{i}$$
تعال معي نستوضح الموضوع بشكل ابسط

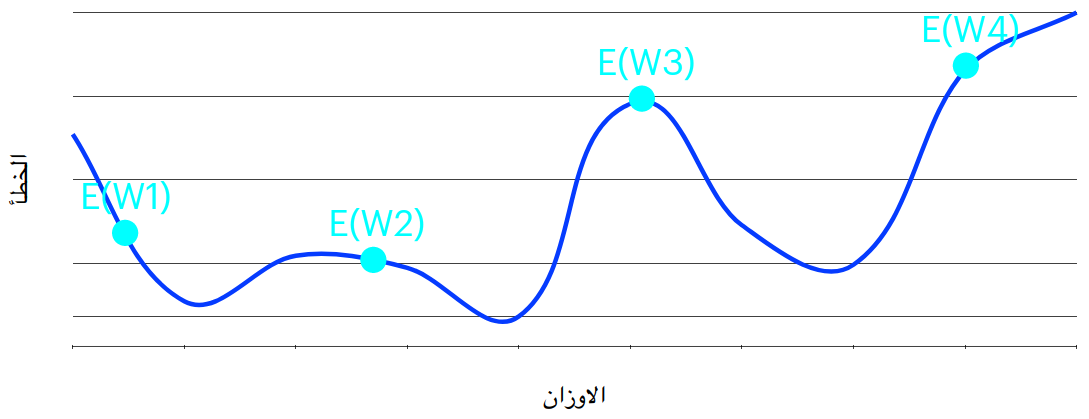
في هذا الرسم نوضح العلاقة بين الخطأ و احد الاوزان ونرى هنا ان عند تغيير الوزن نحصل على قيم مختلفة للخطأ و كذلك يوجد لكل وزن المستوى الخاص به و اذا جمعنا الاوزان كلها سوف ننتهي برسم اشبه بالشكل الآتي ولكن في ابعاد اكثر لا يمكن رسمها

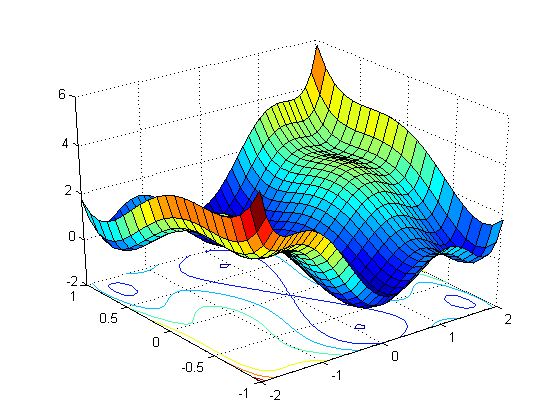
المصدر

الان وبفضل التفاضل يمكننا ان نحدث قيمة الوزن في الاتجاه الذي ينقص الدالة الكلية و هو الاتجاه المعاكس للتفاضل الذي حسبناه بالاعلى وبالتالي يمكننا بعد حساب الخطا ان نحدث قيمة الوزن كما يلي $$ W_t = W_{t-1} - \eta \frac{d}{dW}Error $$ هنا يمكنك ان ترى اننا نحدث قيمة الوزن الجديد بان يصبح الوزن القديم طرح التفاضل مضروب بمعامل η و هو يعبر عن مستوى التعلم او (learning rate) و سوف نتعرض له في مقال اخر بإذن الله
وهكذا تتغير قيمة الاوزان لتصبح قيمة جديدة تتسبب في انخفاض الخطأ بشكل عام.

الشكل الكلي

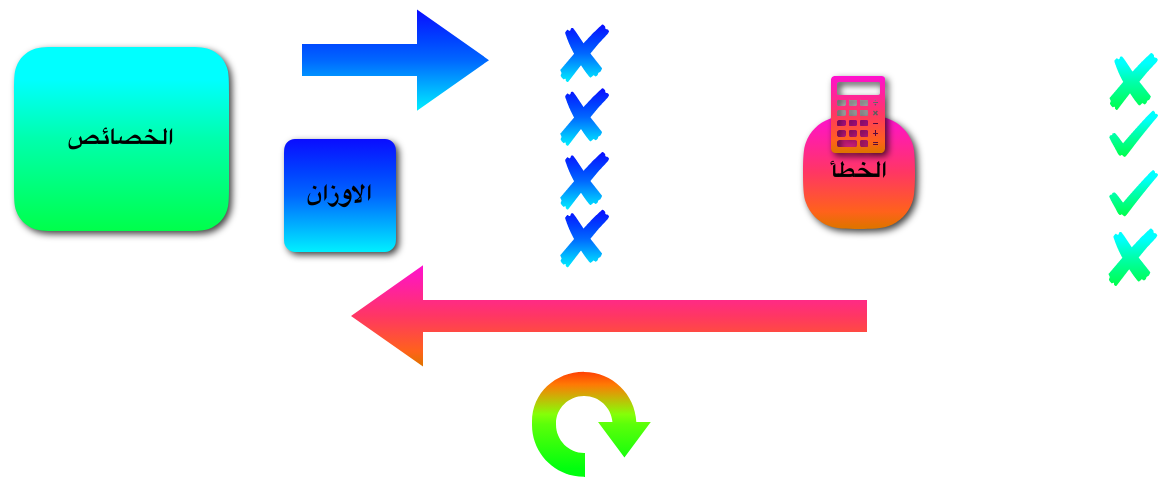
اذا هذا هو تسلسل خطوات النوذج الذي قمنا ببنائه للتو

• تخصيص وزن لكل خاصية
• ابتداء قيمة هذه الاوزان بصفر او الافضل ان نبدأهم بقيم عشوائية
• حساب التوقات بناءا على هذه الاوزان
• حساب الخطأ من هذه التوقعات
• حساب التفاضل بالنسبة لكل وزن وايجاد اتجاه النقصان لكل منهم
• تحديث الاوزان و الرجوع للنقطة الثالثة

يمكنم ان ترى ان هذه السلسلة قد تستمر للأبد، ولكن يتم وضع شروط للتوقف مثل ان تمر بهذه العملية عدد معين من المرات او ان يكون التغيير في معادلة الخطأ اقل من قيمة معينة.

تسمى هذه العملية بالتدريب او التعلم (training/learning) و بعد انتهاء هذه العملية يصبح لدينا اوزان للمتغيرات التي لدينا و يمكننا بناءا عليها ان نتوقع سعر اي منزل قادم بأن نقوم بإدخال متغيرات المنزل في معادلتنا الاساسية بعد حساب الاوزان $$ w_1 x_{1}^{(i)} + w_2 x_{2}^{(i)} + w_3 x_{3}^{(i)} + .... + w_n x_{n}^{(i)} = y^{(i)} $$

اشكال اخرى لتعلم الآلة

ما قمنا بتغطيته للتو هو نوع من انواع تعلم الآلة حيث يكون ما نحاول توقعه قيمة مستمرة يمكن ان تكون اي رقم من سالب مالانهاية إلى مالانهاية و يسمى هذا النوع من النماذج بإسم (regression models) و لكن هذا ليس النوع الوحيد يوجد انواع اخرى تقع جميعها تحت مسمى التعلم تحت الاشراف (suprevised learning)، و هو باختصار وجود بيانات صحيحة نحاول التعلم منها.
وهنا بعض انواع نماذج تعلم الآلة

• التعلم بإشراف (suprevised learning) حيث يتواجد امثلة و يتواجد ايضا التوقع الصحيح لها
  • Regression حيث التوقعات يمكن ان تكون قيم مستمرة
  • Classification حيث التوقعات يمكن انت تكون بين قيم محددة مثل قط او كلب
• التعلم بدون اشراف (unsuprevised learning) حيث يتواجد امثلة ولكن لا يوجد توقع صحيح لها
  • Clustering حيث نقوم بإيجاد مجموعات متشابهة داخل البيانات

الاستنتاج

في هذا المقال تعرضنا بشكل بسيط لماهية تعلم الآلة وكيف يمكن للآلة ان تتعلم من البيانات بشكل مبسط وبتغطية مايوجد خلف مصطلح تعلم الآلة

في هذا المقال حاولت تبسيط بعض المصطلحات للغتنا العربية من اجل تسهيل عملية الشرح ولتبسيط المعلومة، في حالة اي خطأ املائي او اقتراح افضل للترجمة فأنا ارحب جدا بذلك يمكنك التعليق على المقال او مراسلتي لتعديل و تحسين المحتوى، ووفقنا الله وإياكم لما يحب ويرضى.